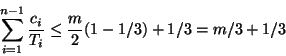DM Schedulability

The analysis of deadline monotonic schedulability is similar to that given above for the EDF case, with a few critical differences.

Lemma 16 (DM demand)   For any busy window $[t, t + \Delta)$ for $\tau _k$ and any task $\tau _i$, the DM demand $W_i$ of $\tau _i$ in the busy window is no greater than $nc_i-\max\{0,c_i-\phi\lambda\}$, where $n=\lfloor (\Delta-\delta_i)/T_i \rfloor +1$, $\phi=nT_i+\delta_i-\Delta$, $\delta_i=c_i$ if $i<k$, and $\delta_i=d_i$ if $i=k$.

Sketch of proof:

The full analysis is given in [5]. We first consider the case where $i<k$, and then consider the special case where $i=k$. Looking at Figure 5, one can see that $W_i$ is maximized for $i<k$ when $\delta_i=c_i$ and $\phi=nT_i+c_i-\Delta$.

Figure 5: Densest possible packing of jobs for $\tau _i$, $i<k$.

For the case $i=k$ it is not possible to have $\delta_i=c_i$. Since $\tau _k$ is the problem job, it must have a deadline at the end of the busy window. Instead of the situation in Figure 5, for $\tau _k$ the densest packing of jobs is as shown in Figure 6. That is, the difference for this case is that the length $\delta_i$ of the tail is $d_i$ instead of $c_i$.

Figure 6: Densest possible packing of jobs for $\tau _k$.

The number of periods of $\tau _k$ spanning the busy window in both is $n=\lfloor (\Delta-\delta_i)/T_i \rfloor +1$, and the maximum contribution of the head is $\epsilon=\max\{0,c_i-\phi\lambda\}$. All differences are accounted for by the fact that $\delta_i=d_i$ instead of $c_i$. $\Box$

Lemma 17 (upper bound on DM load)   For any busy window $[t, t + \Delta)$ with respect to task $\tau _k$ the DM load $W_i/\Delta$ due to $\tau _i$, $i<k$, is at most

$$\begin{eqnarray*} \beta_i = \left\{ \begin{array}{ll} \frac{c_i}{T_i}(1+\frac{T_... ...}{d_k} &\mbox{if}\;\; \lambda<\frac{c_i}{T_i} \end{array}\right. \end{eqnarray*}$$

where $\delta_i=c_i$ for $i<k$, and $\delta_k=d_k$.

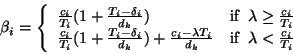
The above lemma leads to the following DM schedulability test.

Theorem 18 (DM schedulability test)   A set of periodic tasks is schedulable on $m$ processors using preemptive deadline-monotonic scheduling if, for every task $\tau _k$,

$$\begin{eqnarray*} \sum_{i=1}^{k-1} \beta_i \leq m(1-\frac{c_k}{d_k}) \end{eqnarray*}$$

where $\beta_i$ is as defined in Lemma 17.

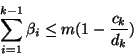
The proof is given in [5]. It is similar to that of Theorem 12, but using the appropriate lemmas for DM scheduling.

Corollary 19 (simplified DM test)   A set of periodic tasks $\tau_1, \ldots, \tau_n$ is schedulable on $m$ processors using preemptive DM scheduling if

$$\begin{eqnarray*} \sum_{i=1}^{n} \frac{c_i}{T_i}(1+\frac{T_i-\delta_i}{d_k}) &\leq& m(1-\lambda)+\lambda \end{eqnarray*}$$

where $\lambda = \max\{\frac{c_i}{d_i}\;\mid\; i=1,\ldots,n\}$, $\delta_i=c_i$ for $i<k$, and $\delta_k=d_k$.

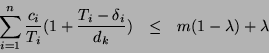
Corollary 19 is proved by repeating the proof of Theorem 18, adapted to fit the definition of $\lambda$.

If we assume the deadline of each task is equal to its period the schedulability condition of Corollary 19 for deadline monotone scheduling becomes a lower bound on the minimum achievable utilization for rate monotone scheduling.

Corollary 20 (RM utilization bound)   A set of periodic tasks, all with deadline equal to period, is guaranteed to be schedulable on $m$ processors, $m\geq 2$, using preemptive rate monotonic scheduling if

$$\begin{eqnarray*} \sum_{i=1}^{n} \frac{c_i}{T_i} \leq \frac{m}{2}(1-\lambda)+\lambda \end{eqnarray*}$$

where $\lambda = \max\{\frac{c_i}{T_i}\;\mid\; i=1,\ldots,n\}$.

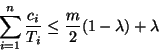
The proof, which is given in [5], is similar to that of Theorem 18.

Analogously to Funk, Goossens, and Baruah[7], Andersson, Baruah, and Jonsson[2] defined a periodic task set $\{\tau_1, \tau_2, \ldots \tau_n\}$ to be a light system on $m$ processors if it satisfies the following properties:

1. $\sum_{i=1}^n \frac{c_i}{T_i}\leq \frac{m^2}{3m-2}$
2. $\frac{c_i}{T_i} \leq \frac{m}{3m-2}$, for $1 \leq i \leq n$.

They then proved the following theorem.

Theorem 21 (Andersson, Baruah, Jonsson[2])   Any periodic task system that is light on $m$ processors is scheduled to meet all deadlines on $m$ processors by the preemptive Rate Monotonic scheduling algorithm.

The above result is a special case of our Corollary 20. If we take $\lambda = m/(3m-2)$, it follows that the system of tasks is schedulable to meet deadlines if

$$\sum_{i=1}^{n} \frac{c_i}{T_i} \leq \frac{m}{2}(1-\frac{m}{3m-2}) + \frac{m}{3m-2} = \frac{m^2}{3m-2}$$

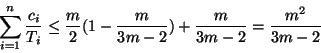
Baruah and Goossens[6] proved the following similar result.

Corollary 22 (Baruah, Goossens[6])   A set of tasks, all with deadline equal to period, is guaranteed to be schedulable on $m$ processors using RM scheduling if $\frac{c_i}{T_i}\leq 1/3$ for $i=1,\ldots,n$ and $\sum_{i=1}^n \frac{c_i}{T_i} \leq m/3$.

This is a slightly weakened special case of our Corollary 20. For $\lambda = 1/3$, it follows that the system of tasks is schedulable to meet deadlines if

$$\sum_{i=1}^{n-1} \frac{c_i}{T_i} \leq \frac{m}{2}(1-1/3) + 1/3 = m/3 + 1/3$$