EDF Schedulability

We want to find a close upper bound on the contribution $W_i$ of each task $\tau _i$ to the demand in a particular window of time. We have bounded the contribution to $W_i$ of the head of the window. We are now ready to derive a bound on the whole of $W_i$ , including the contributions of head, body, and tail for the EDF case.

The tail of a window with respect to a task $\tau _i$ is the final segment, beginning with the release time of the carried-out job of $\tau _i$ in the window (if any). The carried-out job has a release time within the window and its next release time is beyond the window. That is, if the release time of the carried-out job is $t''$, $t'' < t+\Delta <t''+T_i$. If there is no such job, then the tail of the window is null. We use the symbol $\delta$ to denote the length of the tail, as shown in Figure 2.

The body is the middle segment of the window, i.e., the portion that is not in the head or the tail. Like the head and the tail, the body may be null (provided the head and tail are not also null).

Unlike the contribution of the head, the contributions of the body and tail to $W_i$ do not depend on the schedule leading up to the window. They depend only on the release times within the window, which in turn are constrained by the period $T_i$ and by the release time of the carried-in job of $\tau _i$ (if any).

Let $n$ be the number of jobs of $\tau _i$ released in the body and tail. If both body and tail are null, $\Delta=\delta-\phi$, $n=0$, and the contribution of the body and tail is zero. Otherwise, the body and or the tail is non-null, the combined length of the body and tail is $\Delta+\phi-T_i=(n-1)T_i+\delta$, and $n\geq 1$.

Lemma 10 (EDF demand)   For any busy window $[t, t + \Delta)$ of task $\tau _k$ (i.e., the maximal $\lambda$-busy downward extension of a problem window) and any task $\tau _i$, the EDF demand $W_i$ of $\tau _i$ in the busy window is no greater than

$$nc_i+\max\{0,c_i-\phi\lambda\}$$

where $\phi=nT_i+d_i-\Delta$, $n=\lfloor (\Delta-d_i)/T_i \rfloor +1$ if $\Delta\geq d_i$, and $n=0$ otherwise.

Proof: We will identify a worst-case situation, where $W_i$ achieves the largest possible value for a given value of $\Delta$. For simplicity, we will risk overbounding $W_i$ by considering a wide range of possibilities, which might include some cases that would not occur in a specific busy window. We will start out by looking only at the case where $\Delta\geq d_i$, then go back and consider later the case where $\Delta<d_i$.

Looking at Figure 4, it is easy to see that the maximum possible contribution of the body and tail to $W_i$ is achieved when successive jobs are released as close together as possible. Moreover, if one imagines shifting all the release times in Figure 4 earlier or later, as a block, one can see that the maximum is achieved when the last job is released just in time to have its deadline coincide with the end of the window. That is, the maximum contribution to $W$ from the body and tail is achieved when $\delta=d_i$. In this case there is a tail of length $d_i$ and the number of complete executions of $\tau _i$ in the body and tail is $n=\lfloor (\Delta-d_i)/T_i \rfloor +1$.

From Lemma 9, we can see that the contribution $\epsilon$ of the head to $W_i$ is a nonincreasing function of $\phi$. Therefore, $\epsilon$ is maximized when $\phi$ is as small as possible. However, reducing $\phi$ increases the size of the head, and may reduce the contribution to $W_i$ of the body and tail.

Figure 4: Densest possible packing of jobs.

Looking at Figure 4, we see that the length of the head, $T_i-\phi$, cannot be larger than $\Delta-((n-1)T_i+d_i)$ without pushing all of the final execution of $\tau _i$ outside the window. Reducing $\phi$ below $nT_i+d_i-\Delta$ results in at most a linear increase in the contribution of the head, accompanied by a decrease of $c_i$ in the contribution of the body and tail. Therefore the value of $W_i$ is maximized for $\phi=nT_i+d_i-\Delta$.

We have shown that

$$W_i \leq nc_i+\epsilon \leq nc_i+\max\{0,c_i-\phi\lambda\}$$

It is now time to consider the case where $\Delta<d_i$. There can be no body or tail contribution, since it is impossible for a job of $\tau _i$ to have both release time and deadline within the window. If $W_i$ is nonzero, the only contribution can come from a carried-in job. Lemma 9 guarantees that this contribution is at most $\max\{0,c_i-\phi\lambda\}$,

For $n=\lfloor \frac{\Delta-d_i}{T_i} \rfloor +1 = 0$ we have

$$W_i \leq \max\{0,c_i-\phi\lambda\} \leq nc_i+\max\{0,c_i-\phi\lambda\}$$

$\Box$

Lemma 11 (upper bound on EDF load)   For any busy window $[t, t + \Delta)$ with respect to $\tau _k$ the EDF load $W_i/\Delta$ due to $\tau _i$ is at most $\beta_i$, where

$$\begin{eqnarray*} \beta_i = \left\{ \begin{array}{ll} \frac{c_i}{T_i}(1+\frac{T_... ...}{d_k} &\mbox{if}\;\; \lambda<\frac{c_i}{T_i} \end{array}\right. \end{eqnarray*}$$

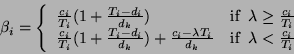
Proof:

The objective of the proof is to find an upper bound for $W_i/\Delta$ that is independent of $\Delta$. Lemma 10 says that

$$\begin{eqnarray*} \frac{W_i}{\Delta} &\leq& \frac{nc_i+\max\{0,c_i-\phi\lambda\}}{\Delta} \end{eqnarray*}$$

Let $\alpha$ be the function defined by the expression on the right of the inequality above, i.e.,

$$\begin{eqnarray*} \alpha(\Delta) &=& \frac{nc_i+\max\{0,c_i-\phi\lambda\}}{\Delta} \end{eqnarray*}$$

There are two cases:

Case 1: $\max\{0,c_i-\phi\lambda\}=0$.

We have $c_i-\lambda\phi\leq 0$, and $\phi\geq c_i/\lambda$. Since we also know that $\phi<T_i$, we have $\lambda\geq\frac{c_i}{T_i}$. From the definition of $n$, we have

$$\begin{eqnarray*} n = \lfloor \frac{\Delta-d_i}{T_i} \rfloor +1 &\leq& \frac{\De... ...qnarray*}&\leq& \frac{c_i}{T_i}(1+\frac{T_i-d_i}{d_k}) = \beta_i \end{eqnarray*}$$

Case 2: $\max\{0,c_i-\phi\lambda\}\neq 0$.

We have $c_i-\lambda\phi>0$. Since $\phi=nT_i+d_i-\Delta$,

$$\begin{eqnarray*} \alpha(\Delta) &=& \frac{nc_i+c_i-\lambda\phi}{\Delta}\\ &=& \frac{n(c_i-\lambda T_i)+c_i-\lambda(d_i-\Delta)}{\Delta} \end{eqnarray*}$$

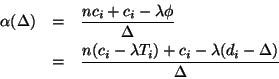
We have two subcases, depending on the sign of $c_i-\lambda T_i$.

Case 2.1: $c_i-\lambda T_i>0$. That is, $\lambda<\frac{c_i}{T_i}$.

From the definition of $n$, it follows that

$$\begin{eqnarray*} n &\leq& \frac{\Delta-d_i}{T_i}+1 = \frac{\Delta-d_i+T_i}{T_i}... ..._i}(1+\frac{T_i-d_i}{d_k})+\frac{c_i-\lambda T_i}{d_k} = \beta_i \end{eqnarray*}$$

Case 2.2: $c_i-\lambda T_i\leq 0$. That is, $\lambda\geq\frac{c_i}{T_i}$.

From the definition of $n$, it follows that

$$\begin{eqnarray*} n &>& \frac{\Delta-d_i}{T_i}\\ \alpha(\Delta) &=& \frac{n(c_i... ...elta}) \\ &<& \frac{c_i}{T_i}(1+\frac{T_i-d_i}{d_k}) = \beta_i \end{eqnarray*}$$

$\Box$

Using the above lemmas, we can prove the following theorem, which provides a sufficient condition for schedulability.

Theorem 12 (EDF schedulability test)   A set of periodic tasks $\tau_1, \ldots, \tau_n$ is schedulable on $m$ processors using preemptive EDF scheduling if, for every task $\tau _k$,

$$\sum_{i=1}^n \min\{1,\beta_i\} \leq m(1-\frac{c_k}{d_k})+\frac{c_k}{d_k}$$ (1)

where $\beta$ is as defined in Lemma 11.

Proof: The proof is by contradiction. Suppose some task misses a deadline. We will show that this leads to a contradiction of (1).

Let $\tau _k$ be the first task to miss a deadline and $[t, t + \Delta)$ be a busy window for $\tau _k$, as in Lemma 7. Since $[t, t + \Delta)$ is $\frac{c_k}{d_k}$-busy we have $W/\Delta > m(1-\frac{c_k}{d_k})+\frac{c_k}{d_k}$. By Lemma 11, $W_i/\Delta\leq \beta_i$, for $i=0,\ldots,n$. Since $t+\Delta$ is the first missed deadline, we know that $W_i/\Delta \leq 1$. It follows that

$$\sum_{i=1}^n \min\{1,\beta_i\} \geq \frac{W}{\Delta} > m(1-\frac{c_k}{d_k})+\frac{c_k}{d_k}$$

The above is a contradiction of (1).$\Box$

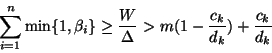
The schedulability test above must be checked individually for each task $\tau _k$. If we are willing to sacrifice some precision, there is a simpler test that only needs to be checked once for the entire system of tasks.

Corollary 13 (simplified EDF test)   A set of periodic tasks $\tau_1, \ldots, \tau_n$ is schedulable on $m$ processors using preemptive EDF scheduling if

$$\begin{eqnarray*} \sum_{i=1}^{n} \min\{1,\frac{c_i}{T_i}(1+\frac{T_i-d_i}{d_{min}})\} &\leq& m(1-\lambda)+\lambda \end{eqnarray*}$$

where $\lambda = \max\{\frac{c_i}{d_i}\;\mid\; i=1,\ldots,n\}$ and $d_{min} = \min\{d_k\;\mid\; i=1,\ldots,n\}$.

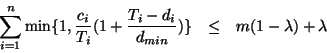
Sketch of proof:

Corollary 13 is proved by repeating the proof of Theorem 12, adapted to fit the definitions of $\lambda$ and $d_{min}$. $\Box$

Goossens, Funk, and Baruah[8] showed the following:

Corollary 14 (Goossens, Funk, Baruah[8])   A set of periodic tasks $\tau_1, \ldots, \tau_n$, all with deadline equal to period, is guaranteed to be schedulable on $m$ processors using preemptive EDF scheduling if

$$\sum_{i=1}^n \frac{c_i}{T_i} \leq m(1-\lambda)+\lambda$$

where $\lambda = \max\{c_i/T_i\;\mid\; i=1,\ldots,n\}$.

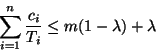
Their proof is derived from a theorem in [7], on scheduling for uniform multiprocessors, which in turn is based on [16]. This can be shown independently as special case of Corollary 13, by replacing $d_i$ by $T_i$.

The above cited theorem of Goossens, Funk, and Baruah is a generalization of a result of Srinivasan and Baruah[18], who defined a periodic task set $\{\tau_1, \tau_2, \ldots \tau_n\}$ to be a light system on $m$ processors if it satisfies the following properties:

1. $\sum_{i=1}^n \frac{c_i}{T_i} \leq \frac{m^2}{2m-1}$
2. $\frac{c_i}{T_i} \leq \frac{m}{2m-1}$, for $1 \leq i \leq n$.

They then proved the following theorem.

Theorem 15 (Srinivasan, Baruah[18])   Any periodic task system that is light on $m$ processors is scheduled to meet all deadlines on $m$ processors by EDF.

The above result is a special case of Corollary 14, taking $\lambda = m/(2m-1)$.