Ramifications

The theorems and corollaries above are intended for use as schedulability tests. They can be applied directly to prove that a task set will meet deadlines with DM or RM scheduling, either before run time for a fixed set of tasks or during run time as an admission test for a system with a dynamic set of tasks. With the simpler forms, one computes $\lambda$ and then checks the schedulability condition once for the entire task set. With the more general forms, one checks the schedulability condition for each task. In the latter case the specific value(s) of $k$ for which the test fails provide some indication of where the problem lies.

The schedulability tests of Theorems 12 and 18 allow preperiod deadlines, but are more complicated than the corresponding utilization bound tests. It is natural to wonder whether this extra complexity gains anything over the well known technique of ``padding'' execution times and then using the utilization bound test. By padding the execution times we mean that if a task $\tau _i$ has execution time $c_i$ and deadline $d_i<T_i$, we replace it by $\tau_i'$, where $c_i'=c_i+T_i-d_i$ and $d_i'=T_i'=T_i$.

With deadline monotonic scheduling, the original task $\tau _k$ can be scheduled to meet its deadline if the following condition holds for $\tau_k'$:

$$\begin{eqnarray*} \frac{c_k'}{T_k}+ \sum_{i<k} \frac{c_i}{T_i} \leq \frac{m}{2}(1-\lambda')+\lambda' \end{eqnarray*}$$

where $\lambda = \max_{i=1}^{n}\{\frac{c_i'}{T_i}, \lambda\}$.

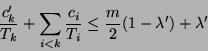
There are cases where this test is less accurate than that of Theorem 18. Suppose we have three processors and three tasks, with periods $T_1=T_2=T_3=1$, deadlines $d_1=d_2=1$, $d_3=1/2$, and compute times $c_1=c_2=c_3=1/4$. Obviously, the tasks are schedulable. However, if we apply the padded utilization test to $\tau_3$, we have $c_3'=1/4+1/2=3/4$, and $\lambda'=3/4$. The test fails, as follows:

$$\begin{eqnarray*} \sum_{i=1}^{2} \frac{1}{4} + \frac{3}{4} = \frac{10}{8} > \frac{3}{2}(1-3/4)+3/4 = \frac{9}{8} \end{eqnarray*}$$

On the other hand this set of tasks passes the test of Theorem 18, as follows:

$$\begin{eqnarray*} \sum_{i=1}^{2} \frac{11}{32} + \frac{1}{2} = \frac{27}{32} <3(1-1/4) = \frac{72}{32} \end{eqnarray*}$$

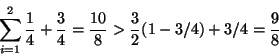
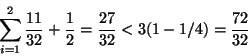
A similar padding technique can be applied for EDF, but again it is sometimes less accurate than Theorem 12.

Of course, these schedulability tests are only sufficient conditions for schedulability. They are like the Liu and Layland $n(2^{1/n}-1)$ utilization bound, both in being very conservative and in still having practical value.

Though the utilization tests are not tight in the sense of being necessary conditions for schedulability, Goossens, Funk, and Baruah[8] showed that the EDF bound is tight in the sense that there is no utilization bound $\hat{U}> m(1-\lambda)+\lambda+\epsilon$, where $\epsilon>0$ and $\lambda=\max\{c_i/T_i\;\mid\; i=0,\ldots,n\}$, for which $U\leq\hat{U}$ guarantees EDF schedulability. Since the EDF utilization bound is tight it is natural to wonder whether the same is true of the RM bound. The following threorem shows that it is not tight.

Theorem 23 (looseness of RM utilization bound)   There exist task sets that are not feasible with preemptive RM scheduling on $m$ processors and have utilization arbitrarily close to $\lambda + m\ln(\frac{2}{1+\lambda})$, where $\lambda$ is the maximum single-task utilization.

Proof: The task set and analysis are derived from Liu and Layland[13]. The difference is that here there are $m$ processors instead of one, and the utilization of the longest-period task is bounded by a $\lambda$.

The task set contains $n=km+1$ tasks where $k$ is an arbitrary integer greater than or equal to 1. The task execution times and periods are defined in terms of a set of parameters $p_1,\ldots,p_{k+1}$ as follows:

$$\begin{eqnarray*} T_{(i-1)*m+j} &=& p_i \;\;\mbox{for}\;\; 1\leq i\leq k, 1\leq ... ...\sum_{i=2}^{k} p_i + 2\sum_{i=2}^{k} p_i + 2p_1\\ &=& 2p_1-T_n \end{eqnarray*}$$

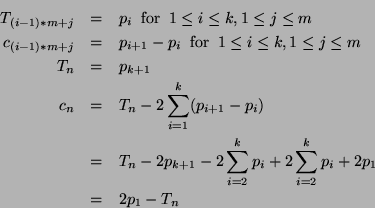
These constraints guarantee that task $\tau_n$ barely has time to complete if all $n$ tasks are released together at time zero. The RM schedule will have all $m$ processors busy executing tasks $\tau_1, \ldots, \tau_{n-1}$ for $\sum_{i=1}^{k}2(p_{i+1}-p_i) = T_n-c_n$ out of the $T_n$ available time units, leaving exactly $c_n$ units to complete $\tau_n$.

If $\frac{c_n}{T_n}=\lambda$, we have

$$\begin{eqnarray*} \lambda T_n &=& c_n = 2p_1 - T_n\\ T_n &=& \frac{2p_1}{1+\lambda} = p_{k+1} \end{eqnarray*}$$

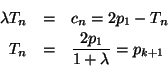
We will choose $p_1,\ldots,p_{k+1}$ to minimize the total utilization, which is

$$\begin{eqnarray*} U &=& \lambda + \sum_{i=1}^{k} m\frac{p_{i+1}-p_i}{p_i}\\ &=& \lambda + m\left((\sum_{i=1}^{k} \frac{p_{i+1}}{p_i})-k\right) \end{eqnarray*}$$

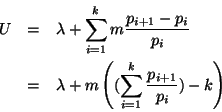
The partial derivatives of $U$ with respect to $p_i$ are

$$\begin{eqnarray*} \frac{\partial U}{\partial p_{1}} &=& m(\frac{2}{(1+\lambda)p_... ...al p_{k}} &=& m(\frac{1}{p_{k-1}}-\frac{2p_1}{(1+\lambda)p_k^2}) \end{eqnarray*}$$

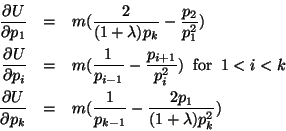
Since the second partial derivatives are all positive, a unique global minimum exists when all the first partial derivatives are zero. Solving the equations above for zero, we get

$$\begin{eqnarray*} \frac{p_2}{p_1} &=& \frac{2}{(1+\lambda)p_k} = \frac{p_{k+1}}{... ...{i+1}}{p_i} &=& \frac{p_i}{p_{i-1}} \;\;\mbox{for}\;\; 1<i\leq k \end{eqnarray*}$$

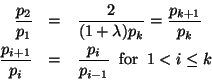
Let $x=\frac{p_{k+1}}{p_{k}}=\cdots=\frac{p_2}{p_1}$. It follows that

$$\begin{eqnarray*} x^k &=& \prod_{i=1}^k \frac{p_{i+1}}{p_i} = \frac{p_{k+1}}{p_1... ...= \lambda + mk\left((\frac{2}{1+\lambda})^{\frac{1}{k}}-1\right) \end{eqnarray*}$$

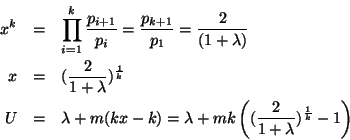
L'Hôpital's Rule can be applied to find the limit of the above expression for large $k$, which is $\lambda + m\ln(\frac{2}{1+\lambda})$. $\Box$

We conjecture that the upper bound on the minimum achievable RM utilization achieved by the example above may be tight.

Srinivasan and Baruah[18] and Andersson, Baruah, and Jonsson[2] showed how to relax the restriction that $c_i/T_i\leq \lambda$ in the utilization tests, for situations where there are a few high-utilization tasks. They propose EDF and RM versions of a hybrid scheduling policy called EDF/US[$\lambda$], where $\lambda=m/(2m-2)$ for EDF and $\lambda = m/(3m-2)$ for RM.

EDF/RM-US[$\lambda$]:

(heavy task rule) If $c_i/T_i > \lambda$ then schedule $\tau _i$'s jobs at maximum priority.

(light task rule) If $c_i/T_i\leq \lambda$ then schedule $\tau _i$'s jobs according to their normal EDF or RM priorities.

They then proved two theorems, which we paraphrase and combine as follows:

Theorem 24 (SB[18] & ABJ[2])   Algorithm EDF/RM-US[$\lambda$] correctly schedules on $m$ processors any periodic task system with total utilization $U\leq m\lambda$.

The proof is based on the observation that the upper bound on total utilization guarantees that the number of heavy tasks cannot exceed $m$. The essence of the argument is that the algorithm can do no worse than scheduling each of the heavy tasks on its own processor, and then scheduling the remainder (which must must be light on the remaining processors) using the regular EDF or RM algorithm.

The above result can be generalized slightly, as follows:

Theorem 25   Algorithm EDF/RM-US[$\lambda$] correctly schedules on $m$ processors any periodic task system such that only $k$ tasks ( $0 \leq k \leq m$) have utilization greater than $\lambda$ and the utilization of the remaining tasks is at most $(m-k)(1-\lambda)+\lambda$ for EDF and at most $((m-k)/2)(1-\lambda)+\lambda$ for RM.

Proof: As argued by Srinivasan and Baruah, the performance of this algorithm cannot be worse than an algorithm that dedicates one processor to each of the heavy tasks, and uses EDF or RM to schedule the remaining tasks on the remaining processors. The utilization bound theorem then guarantees the remaining tasks can be scheduled on the remaining processors. $\Box$

If there is a need to support preperiod deadlines, this idea can be taken further, by changing the ``heavy task rule'' to single out for special treatment a few tasks that fail the test conditions of one of our schedulability tests that allows preperiod deadlines, and run the rest of the tasks using EDF or DM scheduling.