Bounding Carry-In

We now try to derive an upper bound on the load of a window leading up to a missed deadline. If we can find such an upper bound $\beta > W/\Delta$ it will follow from Lemma 3 that the condition $\beta \leq m - (m-1)c_k/d_k$ is sufficient to guarantee schedulability. The upper bound $\beta$ on $W/\Delta$ is the sum of individual upper bounds $\beta_i$ on the load $W_i/\Delta$ due to each individual task in the window. It then follows that

$$\frac{W}{\Delta} = \sum_{i=1}^n \frac{W_i}{\Delta} < \sum_{i=1}^n \beta_i$$

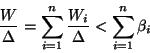
While our first interest is in a problem window, it turns out that one can obtain a tighter schedulability condition by considering a well chosen downward extension $[t, t + \Delta)$ of a problem window, which we call a window of interest.

For any task $\tau _i$ that can execute in a window of interest, we divide the window into three parts, which we call the head, the body, and the tail of the window with respect to $\tau _i$, as shown in Figure 2. The contribution $W_i$ of $\tau _i$ to the demand in the window of interest is the sum of the contributions of the head, the body, and the tail. To obtain an upper bound on $W_i$ we look at each of these contributions, starting with the head.

The head is the initial segment of the window up to the earliest possible release time (if any) of $\tau _i$ within or beyond the beginning of the window. More precisely, the head of the window is the interval $[t,t+\mbox{min}\{\Delta,T_i-\phi)\})$, such that there is a job of task $\tau _i$ that is released at time $t'=t-\phi$, $t<t'+T_i<t+T_i$, $0\leq\phi<T_i$. We call such a job, if one exists, the carried-in job of the window with respect to $\tau _i$. The rest of the window is the body and tail, which are formally defined closer to where they are used, in Section 5.

Figure 2: Window with head, body, and tail.

Figure 2 shows a window with a carried-in job. The release time of the carried-in job is $t'=t-\phi$, where $\phi$ is the offset of the release time from the beginning of the window. If the minimum interrelease time constraint prevents any releases of $\tau _i$ within the window, the head comprises the entire window. Otherwise, the head is an initial segment of the window. If there is no carried-in job, the head is said to be null.

The carried-in job has two impacts on the demand in the window:

1. It constrains the time of the first release of $\tau _i$ (if any) in the window, to be no earlier than $t+T_i-\phi$.

2. It may contribute to $W_i$.

If there is a carried-in job, the contribution of the head to $W_i$ is the residual compute time of the carried-in job at the beginning of the window, which we call the carry-in. If there is no carried-in job, the head makes no contribution to $W_i$.

Definition 4 (carry-in)   The carry-in of $\tau _i$ at time $t$ is the residual compute time of the last job of task $\tau _i$ released before $t$, if any, and is denoted by the symbol $\epsilon$.

Figure 3: Carry-in depends on competing demand.

The carry-in of a job depends on the competing demand. The larger the value of $\phi$ the longer is the time available to complete the carried-in job before the beginning of the window, and the smaller should be the value of $\epsilon$. We make this reasoning more precise in Lemmas 5 and 9.

Lemma 5 (carry-in bound)   If $t'$ is the last release time of $\tau _i$ before $t$, $\phi = t - t'$, and $y$ is the sum of the lengths of all the intervals in $[t',t)$ where all $m$ processors are executing jobs that can preempt $\tau _i$, then

1. If the carry-in $\epsilon$ of task $\tau _i$ at time $t$ is nonzero, then $\epsilon=c_i-(\phi-y)$.
2. The load of the interval $[t',t)$ is at least $(m-1)(\phi - c_i + \epsilon)/\phi + 1$.

Proof: Suppose $\tau _i$ has nonzero carry-in. Let $x$ be the amount of time that $\tau _i$ executes in the interval $[t', t'+\phi)$. For example, see Figure 3. By definition, $\epsilon = c_i-x$. Since the job of $\tau _i$ does not complete in the interval, whenever $\tau _i$ is not executing during the interval all $m$ processors must be executing other jobs that can preempt that job of $\tau _i$. This has two consequences:

1. $x = \phi - y$, and so $\epsilon=c_i-(\phi-y)$

2. The load of the interval $[t', t'+\phi)$ is at least $(my + (\phi - y))/\phi$.

From the first observation above, we have $y = \phi-c_i+\epsilon$. Putting these two facts together gives

$$\frac{my + (\phi - y)}{\phi} = (m-1)\frac{y}{\phi} + 1 = (m-1)\frac{\phi-c_i+\epsilon}{\phi} + 1$$

$\Box$

Since the size of the carry-in, $\epsilon$, of a given task depends on the specific window and on the schedule leading up to the beginning of the window, it seems that bounding $\epsilon$ closely depends on being able to restrict the window of interest. Previous analysis of single-processor schedulability (e.g., [13,3,10,11]) bounded carry-in to zero by considering the busy interval leading up to a missed deadline, i.e., the interval between the first time $t$ at which a task $\tau _k$ misses a deadline and the last time before $t$ at which there are no pending jobs that can preempt $\tau _k$. By definition, no demand that can compete with $\tau _k$ is carried into the busy interval. By modifying the definition of busy interval slightly, we can also apply it here.

Definition 6 ($\lambda$-busy)   A time interval is $\lambda$-busy if its combined load is at least $m(1-\lambda)+\lambda$. A downward extension of an interval is an interval that has an earlier starting point and shares the same endpoint. A maximal $\lambda$-busy downward extension of a $\lambda$-busy interval is a downward extension of the interval that is $\lambda$-busy and has no proper downward extensions that are $\lambda$-busy.

Lemma 7 (busy window)   Any problem interval for task $\tau _k$ has a unique maximal $\lambda$-busy downward extension for $\lambda=\frac{c_k}{d_k}$.

Proof: Let $[t_0,t_0+d_k)$ be any problem window for $\tau _k$. By Lemma 3 the problem window is $\lambda$-busy, so the set of $\lambda$-busy downward extensions of the problem window is non-empty. The system has some start time, before which no task is released, so the set of all $\lambda$-busy downward extensions of the problem window is finite. The set is totally ordered by length. Therefore, it has a unique maximal element. $\Box$

Definition 8 (busy window)   For any problem window, the unique maximal $\frac{c_k}{d_k}$-busy downward extension whose existence is guaranteed by Lemma 7 is called the busy window, and denoted in the rest of this paper by $[t, t + \Delta)$.

Observe that a busy window for $\tau _k$ contains a problem window for $\tau _k$, and so $\Delta\geq d_k$.

Lemma 9 ($\lambda$-busy carry-in bound)   Let $[t, t + \Delta)$ be a $\lambda$-busy window. Let $t-\phi$ be the last release time of $\tau _i$, where $i \neq k$, before time $t$. If $\phi\geq d_i$ the carry-in of $\tau _i$ at $t$ is zero. If the carry-in of $\tau _i$ at $t$ is nonzero it is between zero and $c_i-\lambda\phi$.

Proof: The proof follows from Lemma 5 and the definition of $\lambda$-busy. $\Box$