Introductory Seminar on Research (CIS 5935)

Fall Term 2007

Outline

What kinds of research I have done in the past?
What is the main direction of my research?
What, specifically, am I working on now?
Some details on current projects

Elements of good CS research:

a problem or application that people care about and are likely to use
a new algorithm, idea, or question
a sound abstract model, with analysis pushed to the limit of what theory can do
an implementation study, to:
- verify feasibility
- resolve, empirically, any issues that the theory cannot
- encourage use, by providing a working product
if full-scale implementation is not practical, do simulations:
- resolve, empirically, issues that the theory cannot

Past work

theory: computability, computational complexity, P&NP
algorithms: pattern matching, parsing, priority queues
compilers: semantic analysis, parsing, code generation, Ada, worst-case execution time analysis, reducing context switches
OS: real-time kernels, threads, multiprocessing, standards (POSIX/UNIX)
real time: kernels, scheduling, programming languages

Examples of past projects

exploratory development -- OS's and PL's

GNAT Ada compiler
→ concurrency
→ optimization
→ Java bytecode target
→ RT Linux target
GNARL runtime system (Ada) → optimization, portability
Ada language standard → real-time extensions, AST, locking
POSIX threads (C) - FSU pthreads library
POSIX Ada binding (Ada) → sockets, test suite
Linux (C) → real time extensions

theory - real-time schedulability analysis

concurrency and resource control
multiprocessor scheduling models
timing analysis

Examples of student involvements

Real-time Serial I/O driver (MS, Goyal - now a VP at Oracle)
Prediction of Worst-Case Execution Times (PhD, Harmon - professor at FAMU)
Ada 83 multi-tasking optimizations (PhD, Giering - IBM/Rational)
Ada 95 tasking optimizations (PhD, Oh - professor in Korea)
Real-time nested DB transactions (PhD, Moon - professor in Korea)
RT Linux Ada kernel (MS, Shen - Microsoft , device driver group)
RT Linux Sporadic Server (MS, Shi - Sun, Java technology group)
Multiprocessor schedulability testing (students Fisher from UNC and Cirinei from Pisa)
Modeling device driver effects in demand-based schedulability analysis (FSU students Lewandowski and Stanovich)

What is my main current research area?

"real-time systems"

What is "real time"?

Is achieving correct timing a primary consideration in the design?
Does the computer system need to synchronize with external entities?
Can a timing error cause the entire system to fail? e.g.
- if output is produced to early?
- if output is produced too late?
- if time between input and output is too long?

Examples of real time systems

autopilot
nuclear reactor monitoring system
chemical plant control system
remotely piloted vehicle
robot
multi-media player
washing machine, TV, automobile
stock market analysis system
video surveillance system

Real-time systems research

Goal: Designing and implementing systems with control over execution timing
-- i.e., over when certain steps of a computation are executed, relative to events in the real world.

Ideal: should be able to design and code a system with as much confidence that timing will be correct as that output values will be correct

Order of importance:

predictability
reliability
speed, efficiency

X + predictable/controllable timing = real-time X

Core problems

Evolutionary trends in hardware and software have made predicting execution timing increasingly difficult.
requires cooperation of all levels of the computer/system
- application program
- programming language implementation
- operating system
- hardware
theory:
- models of computation -- require simplifications
- scheduling algorithms, concurrency control/resource allocation algorithms
- analysis of schedulability (for each algorithm)
practice:
- implementations
- performance testing
- trial applications

Current research projects

real-time multiprocessor scheduling
- schedulability analysis (theory)
- partitioned and global models
- concurrency control
- implementation and performance studies
real-time device driver architecture
- 4-year NSF grant (now in 3rd year): with Kartik Gopalan & Andy Wang
- RAs: Mark Stanovich, maybe budget for one more?
- objective: structure and schedule device drivers to make real-time scheduling more predictable for applications
- device drivers course
- looking for applications

Real-time device driver architecture

Theory on real-time scheduling is already strong
- workload must fit one of several abstract models
- scheduling must be according to one of several well analyzed policies/algorithms
- can prove timing constraints will always be met, or determine frequency/probability of failure
Problems remain with device drivers
- real-time applications
  - can be prevented from using CPU by device driver interference
  - can be delayed waiting for I/O that is scheduled by the driver
- scheduling of driver on CPU uses special OS mechanisms
  - is hierarchical, does not fit models of theory
- workload of driver on CPU is determined by device
  - does not fit neat theoretical models
- drivers are device-centric
  - can preempt and block application threads/processes on CPU
  - may schedule I/O to maximize use of device, rather than meet deadlines
- devices also get involved in scheduling
  - little to no control by OS
  - interactions make analysis difficult

Approach to research

study some real drivers in Linux

analyze their workload
- read driver code to see logic
- insert instrumentation code to get actual timings
- run benchmarks (tests) and gather data
how to they compete with application threads for CPU time?
how do they hold up applications waiting for I/O?
try to match workload to abstract models
- what are the "jobs" and the "tasks"?
- what is their execution pattern (periodic, sporadic, what?)
- what are their scheduling requirements?

look at how the OS schedules them
- does it fit any analyzed formal models?
- if not, can we analyze it?
- if not, can we change kernel to fit a nicer model?
try to analyze the drivers interactions with real-time threads
- check predictions against actual performance
look for ways to improve analyzability/performance
- in analysis techniques
- in driver design
- in OS support for drivers
  - extend/modify kernel "API" for drivers
  - provide application-level controls?

References:

See Modeling device driver effects in real-time schedulability analysis: Study of a network driver, Lewandowski, Stanovich, Baker, Gopalan, Wang (RTAS 2007)
See Fitting Linux device drivers into an analyzable scheduling framework, Baker, Wang, Stanovich (ECRTS OSPERT 2007)

Example: Effect of I/O activity on real-time response

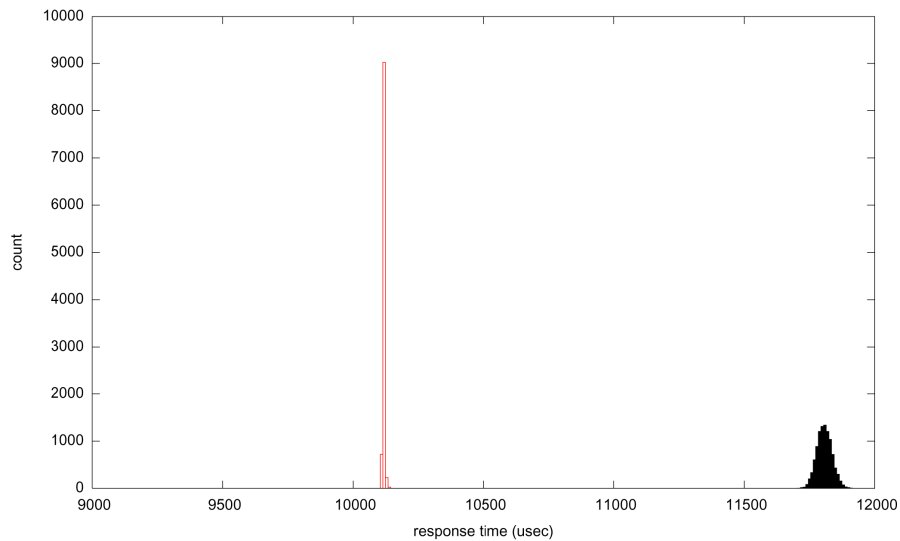
Response time distributions of a task with 100 msec. period and 10 msec. execution time, with interference from network and disk drivers.

red: task has higher priority than device drivers
black: task has lower priority than device drivers

Example: Empirical estimation of interference due to network driver

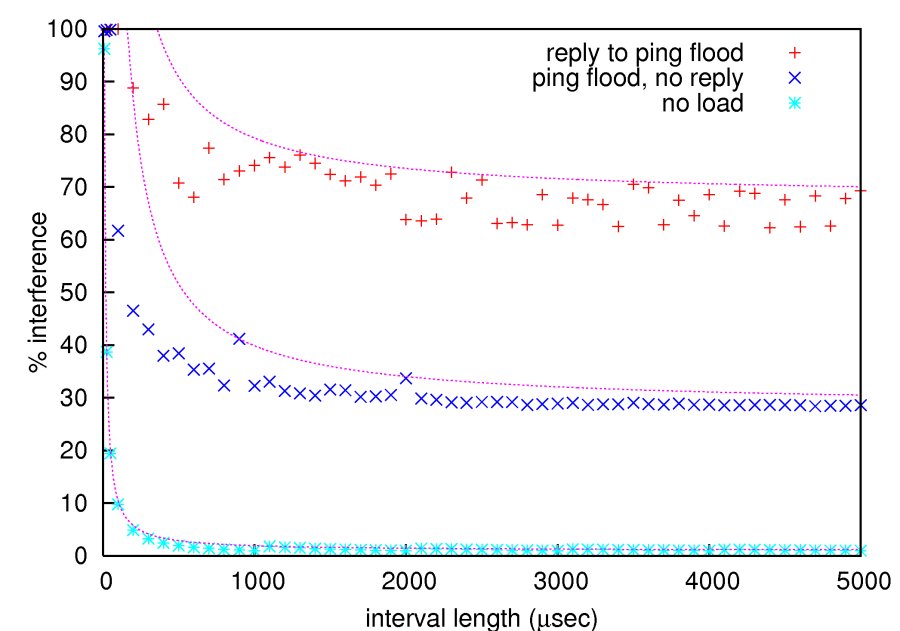
Interfering load = maximum % of CPU time consumed by higher priority activities over time all intervals of a given length.

Example: A model for observed interference

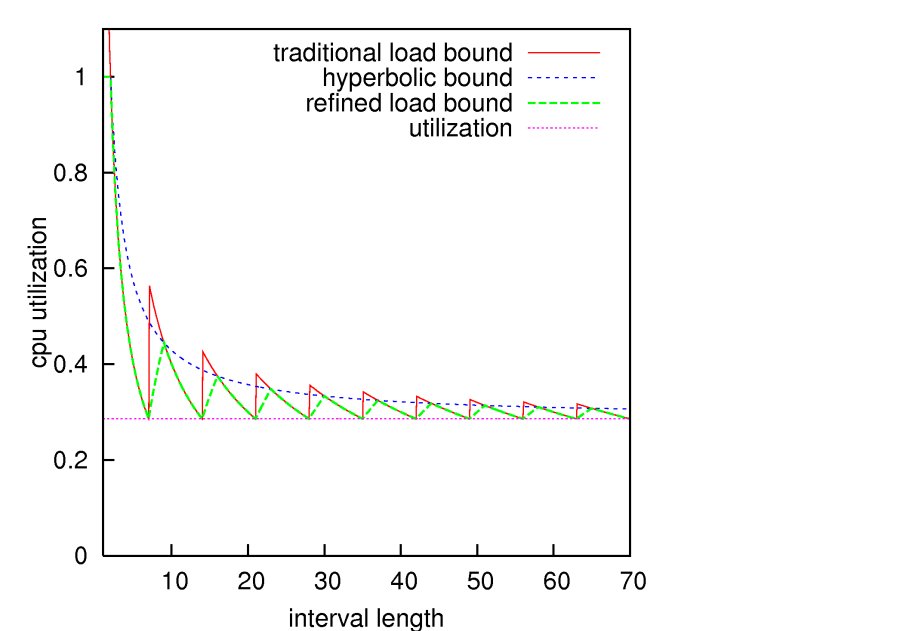
Empirical upper bounds on interfering load due to device drivers can be fittedhave similar shape to periodic task.

Permits combining device driver interference with analysis of periodic tasks

Research on Real-Time Disk I/O Drivers - Mark Stanovich

Long response time of device means
- small CPU time interference from device driver
- high impact of device I/O scheduling on
  - deadlines of I/O bound tasks
  - system disk throughput
  - a trade-off
Built-in scheduler of disk means
- more precise information on head and data positions permits more effective scheduling
- scheduler algorithm is unknown, complex, not easy to infer, varies between disks
- not designed for real-time predictability
What should the device driver do to support real-time applications?

SMP Schedulability Analysis

multiprocessors, including multi-core becoming more common
schedulability theory not well developed, relative to single processor
- core result for single processor, on "critical instants", does not apply
traditional method: partioned scheduling (queue per processor)
- apply single-processor scheduling on each CPU
- optimal partitioning is NP-hard
- first-fit comes within 50% of optimal, usually much better
- worst case: breakdown at 50% of optimal processor utilization
global (single queue) scheduling
- originally deprecated, due to Dhalls' effect (see below)
- recently shown to be competitive with partitioning
- intuitively is more efficient, since CPUs are never idled when there is work to be done
- interactions with memory cache are subject to debate

References:

EDZL Scheduling Analysis, Cirinei, Baker (ECRTS 2007)
A Necessary and Sometimes Sufficient Condition for the Feasibility of Sets of Sporadic Hard-Deadline Tasks, Baker, Cirinei (RTSS 2006)
Brute-Force Determination of Multiprocessor Schedulability for Sets of Sporadic Hard-Deadline Tasks, Baker, Cirinei (submitted)

Real-Time Scheduling Terms

job = unit of schedulable work
- a procedure, and data on which it executes
- an execution time (generally not known exactly, but usually with known upper bound)
- a deadline (hard or soft)
task τ_i = sequence of jobs J_i,j — a.k.a. "thread", "process"
periodic task = job release times are separated by a constant (the task period)
sporadic task = job release times are separated by at least a constant (the task period)
aperiodic task = not a periodic or sporadic task
- some load limiting constraint needed to ensure schedulability
- e.g., load bound function (see below)
utilization of a task is average execution time needed per unit of real time = c_i/T_i
(one of several metrics)
demand of a task in a time interval is the amount of processor time used by the task in the interval
load = demand / interval_length
any upper bound on the load for a given interval length is useful for predicting schedulability

``Dhall Effect'' with EDF/DM Scheduling on MP

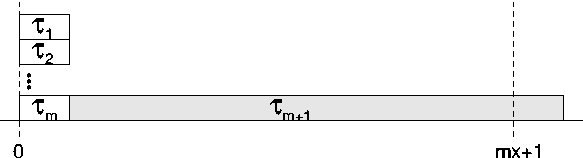
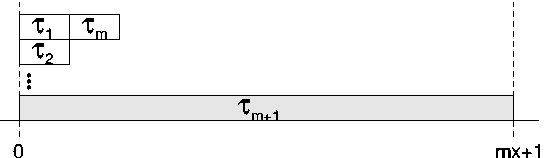
This is only a problem when we have some tasks with very high local utilization.

This example shows worst-case achievable multiprocessor utilization can be arbitrarily close to 1, compared to ideal value of m. Until recently, it was used as an excuse for using partitioned scheduling on multiprocessors. However, the example depends on mixing tasks with extremely low and extremely high utilization (or ratio of compute time to deadline). Intuitively, we know we can achieve higher utilization when we have only smaller tasks.

Global Schedulability Tests - Basic Idea

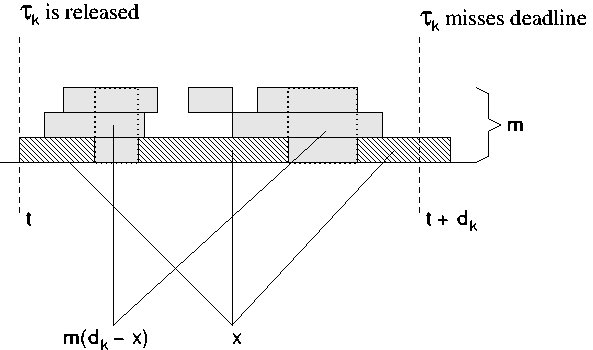
Load-Based Schedulabity Analysis

Find a lower bound μ on the load of a window leading up to a deadline that is necessary for the deadline to be missed.
Find an upper bound β on the load of such a window that can be generated by a given task set.
If β < μ the task set must be schedulable.

There are several variations as to how we define "load" that allow different refinements in analysis.

Example: Generalized Fixed-Priority Density Test

A system of N independent sporadic tasks can be scheduled to meet all deadlines on M processors using preemptive global fixed task-priority scheduling if (but not necessarily only if), for every task τ_k there exists λ≥λ_k such that one of the following criteria is satisfied

n
∑
i=1

min(β^λ_k(i), 1 - λ) < m (1- λ)

n
∑
i=1

min(β^λ_k(i), 1 - λ) = m (1- λ) and ∀ i β^λ_k(i) ≤ (1- λ) ⇒ β^λ_k(i) = 0

where

β^λ_k(i)

def
=

0			if	i ≥ k
u_i(1 + max(0,	p_i-e_i d_k	))	if	u_i≤λ and i < k
u_i(1 + max(0,	p_i-e_i+d_i(1- λ/u_i) d_k	))	if	u_i>λ and i < k

This is one of several results, which have gradually provided better techniques for verifying schedulability of task systems on multiprocessors.

Unfortunately, they do not cover all the cases. When it comes to evaluating how well they do, we look at performance in simulations on large numbers of task sets.

Example simulation experiment:
BC Test for Deadline Monotonic Scheduling on 4 CPUs

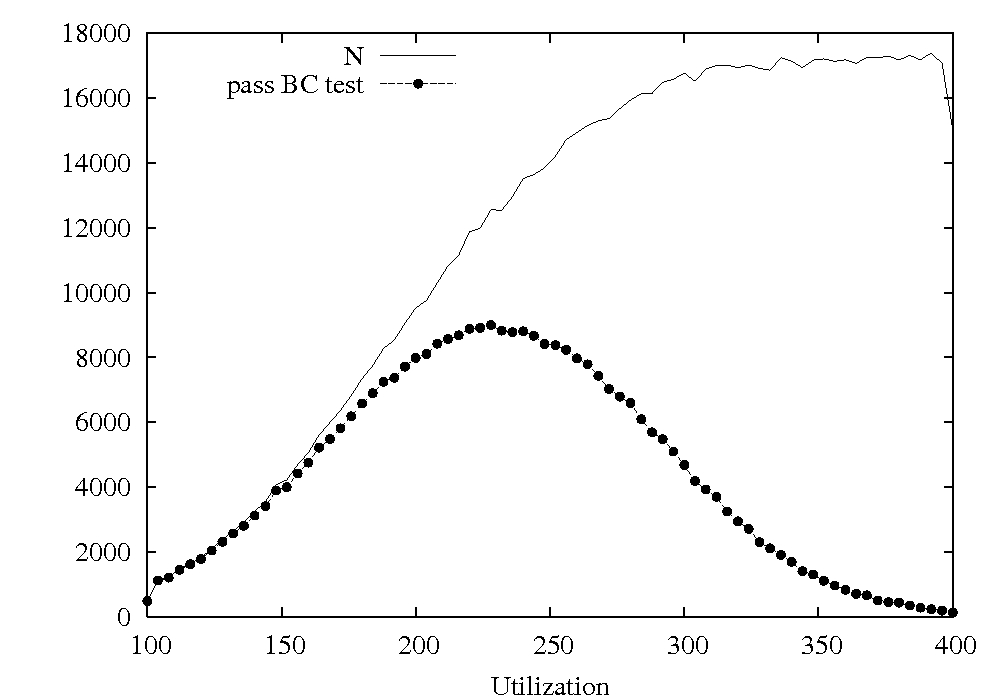
How many of the task sets that could not be proven schedulable are not schedulable?

Hierarchy of possibilities for a task set

schedulable to meet all deadlines by given method
- proven schedulable by a given test
- schedulable, but not proven
feasible (there exists a schedule that meets deadlines) but not schedulable by given method
- proven feasible (how?)
- feasible, but not proven
infeasible (there is an arrival sequence for which no schedule can meet all deadlines)
- infeasible, but not proven
- proven infeasible

Some directions for research

Theory:

Tighten analysis of global scheduling algorithms to more precisely determine schedulability
Also look at other measures, such as response time, lateness, and number of context switches
Look at new algorithms.

Experiments:

Shed light on real magnitude of cache effects and scheduler lock contention
Is global scheduling workable? Up to how many processors?
Look at various SMP and multicore architectures