Lower Bounds for Sorting

All our sorting has been comparison sorting:

Given a_i, a_j from <a₁, a₂, a₃, ...,a_n> we perform one of the comparisons:

1. a_i < a_j

2. a_i £ a_j

3. a_i = a_j

4. a_i > a_j

5. a_i ³ a_j

To determine their relative order. If we assume all the elements are distinct, then we only need to consider a_i £ a_j . "=" is excluded and ³ , £ , >, <,  are equivalent.

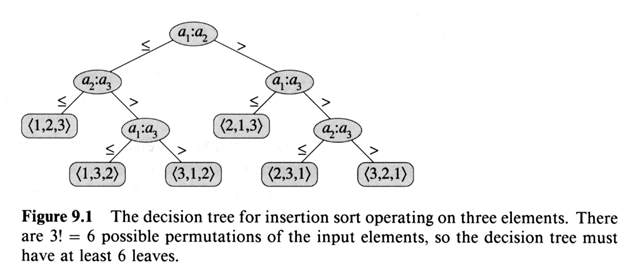
This pictorially shows all possible comparisons a_i : a_j and all possible outcomes < 1, 3, 2 >

In a decision tree each leaf is a permutation of the input < p (1), p (2), ... p (n) >.

Doing a comparison sort: trace a singe path (based on the actual comparison results) from the root to one of the leaves. This is the execution path for the sort. Note that different sorting algorithms will use different comparisons, and use them in different orders.

If length[A] = n. then there are n! different permutations on n distinct elements.

Lower bound on comparison sorting -- worst case:

Any decision tree that sorts n elements has height W ( n lg n ). 'h' = height of decision tree that sorts n elements. Since we have n! permutations and so n! leaves, and since decision trees are binary trees, we have:

n! £  2^h (may not be complete, in fact won't be)

h ³ lg ( n! )

Stirling: n! = Ö( 2 n ) ( n/e )ⁿ ( 1 + Q ( 1/n ) ) > ( n/e )ⁿ

h ³ lg ( n! ) > lg ( n/e )ⁿ

= n ( lg n - lg e )

= n lg n - n lg e

=  W ( n lg n )

Since the height of the decision tree gives the worst-case running time of comparison sorts, we have that Heap-sort and Merge-sort are asymptotically optimal comparison sorts. (both have running times of O ( n lg n ) as upper bounds.