Representation of Polynomials

 

Polynomial A (x) =
n - 1
å
j = 0 		 aj xj
yields the coefficient representation of A (x) with d-b n: (a0, a1, ...,an-1) a vector of the coefficients. Consider, given a0, a1, ...,an-1 as a representation of A (x) evaluation A (x0). We can use Horner's rule to do so in Q (n) :

a0 + x0(a1 + x0(a2 + x0 (a3+ ..... + x0(an-2 + x0  an-1)

This can easily be written as an iterative algorithm with a single loop of length n ( 0 to n-1 .) Adding A (x) and B (x) is again Q (n).  (c0, c1, ...,cn-1) with cj = aj + bj.

What about the multiplication of two d-b  n polynomials A (x) and B (x)? Polynomial multiplication via the "school book algorithm is Q (n2), and C = (c0, c1, ...,c2n-2) is obtained through convolution:

 

  cj =
j
å
k = 0 		 ak bj-k

C = A Ä B ( Ä means convolution). We study fast algorithm for convolution! A point-value representation of A (x) a polynomial of d - b n point-value pairs:

{ ( x0, y0), ( x1, y1), ..., ( xn-1, yn-1) }

with all the x's distinct and y j= A (xj) . Note: any set of n distinct x's can be used, so there are many point-value representations of A (x)! By using Horner's rule, one can evoluate A (x) at a point in Q (n) time, so conversion from coefficient to point-value takes Q (n2) time using Horner's rule n times. We will choose the x's in a special way to obtain a Q (n lg n) algorithm. Given the point-value representation and computing the coefficient representation of A (x) is called interpolation.

Theorem 32.1: For any set { ( x0, y0), ( x1, y1), ..., ( xn-1, yn-1) } of n p - v pairs there is a unique d - b n polynomial, A (x) such that y i= A (xi) for i = 0, ..., n - 1.

Proof: write out A (x0) = y0 , A (x1) = y1 , ..., A (xn-1) = yn-1 as:

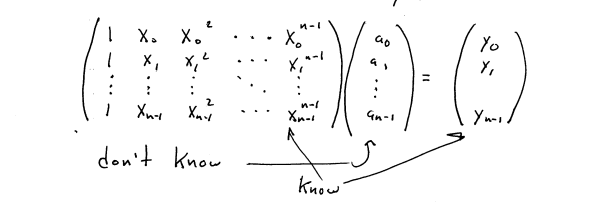
The matrix V (x0, x1, ...,xn-1) is called a Vandermonde matrix and:

 det (x0, x1, ...,xn-1)  =
å
j < k 		 ( xk - xj )

 det (x0, x1, ...,xn-1) ¹ 0 since all the x's are distinct. So the system has a solution:

a = V (x0, x1, ...,xn-1)-1 y

so the a's can be uniquely found!! Solving such a linear system takes Q ( n3 ) time, but we can interpolate faster:

LaGrange formula: given p - v, A ( x ) =

n - 1
å
k = 0 
 Yk  P ( x - xj)
 j < k 
     P ( xk - xj)
j < k 

can show that A ( x ) is a d - b n polynomial and A ( xi ) = yi . This takes Q ( n2 ) time.

A ( x ) ® { ( x0, y0 ), ( x1, y1 ), ..., ( xn-1, yn-1 ) }

B ( x ) ® { ( x0, y0' ), ( x1, y1' ), ..., ( xn-1, yn-1' ) }

Consider C ( x ) = A ( x ) + B ( x ) so

C  ( x ) ® { ( x0, y0 + y0' ), ( x1,  y1 + y1' ), ..., ( xn-1,  yn-1 + yn-1' ) }

and conversion takes  Q ( n ) time. What about multiplication of A ( x ) and B ( x ) both d - b n polynomials? C ( x ) = A ( x ) B ( x ) is a d - b 2n - 1, so we must augment the number of p - v pairs used to represent A ( x ) and B ( x ):

A ( x ) ® { ( x0, y0 ), ( x1, y1 ), ..., ( x2n-2, y2n-2 ) }

B ( x ) ® { ( x0, y0' ), ( x1, y1' ), ..., ( x2n-2, y2n-2' ) }

C  ( x ) ® { ( x0, y0 y0' ), ( x1,  y1 y1' ), ..., ( x2n-2,  y2n-2 y2n-2' ) }

 is Q ( n ) time. If we can find a fast way to convert coefficients to p - v pairs, use the  Q ( n )  multiplication on p - v pairs, and convert back, we will have a very fast algorithm. We do so by choosing the points for the p -  v pairs very carefully. These points are the complex roots of unity.

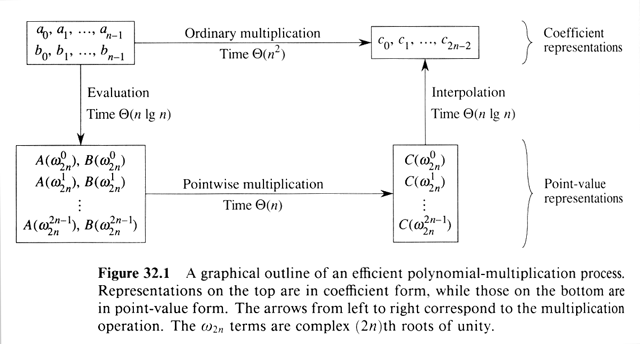
To multiply A ( x ) B ( x ) we:

  1. Use the coefficient representation, but up to degree bound 2n by padding with zeros.
  2. Compute the p - v of A ( x ) and B ( x ) at the 2n roots of unity via the FFT.
  3. Do point wise multiplication.
  4. Interpolate back from the 2n roots of unity to a coefficient representation via inverse DFT

 
Polynomials and the FFT - 2 of 4