Bounding Summations
Mathematical Induction:
To Prove:
when n = 1, the sum equals (1 ( 1 + 1 )) / 2 = 1 : so this checks out.
Assume true for n, and the prove n + 1
n+1
å i =
i = 1 |
n
å i + ( n + 1 ) =
i = 1 |
(n (n + 1 ))/2 + n +1 |
|
= |
(n + 1)[n/2 + 1] |
|
= |
(n + 1)( (n + 2)/2)) done! |
Induction for bounds:
Prove
recall
|
|
(3n+1 - 1 )/(3 - 1 ) = (3n+1 - 1 )/2 |
must show that
|
|
c 3 n for some c ³ 0 and n ³
n0 |
first
|
|
1 £ c 3 0 = c,
c = 1 works for n = 0 |
assume
then n + 1
n+1
å 3k =
i = 0 |
n
å 3k + 3n+1 £
i = 0 |
c 3 n + 3 n+1 |
|
= |
(1/3 + 1/c) c 3 n+1 |
|
£ |
c 3 n+1 |
provided that (1/3 + 1/c) £ 1 Þ 1/c £ 1 - 1/3 Þ c ³ 3/2
Some Tricks:
bound each term
n
å k £
k = 1 |
n
å n = n2
k =1 |
n
for å ak,
if ak £ amax "
k = 1....n , £
i = 1 |
n
å amax = namax
k = 1 |
bound with Geometric Series
if ak+1 / ak £ r " k then ak+1 £
rak £ r2ak-1... £ a0rk+1
therefore
n
å ak £
k = 0 |
n
å a0rk
= a0((rk+1 -1) / (1 - r))
k = 0 |
| if r < 1 then a0( 1 / (r _ 1) ) = |
¥
å a0rk
k = 0 |
Example
¥
å k / 3k =
k = 0 |
¥
å ak
k = 0 |
(ak+1) / ak = (k + 1) / 3k+1 * 3k / k = (k + 1) / k * 1/3 £ 1/3 * 2/1 = 2/3 as (k + 1 ) / k £ 2 (equality when k = 1)
¥
å k / 3k £
k = 1 |
¥
å 1/3 (2/3)k = 1/3 ( 1 / (1 - 2/3)) = 1
k = 1 |
Harmonic Series (as a counter example)
¥
å k-1 =
k = 1 |
lim
n ® ¥ |
n
å k-1 = lim Q( ln n) = + ¥
n ® ¥
k = 1 |
So this Diverges
(ak+1) / ak = (1 / (k + 1)) / 1/k = k / (k +1) < 1 but not!! £ c < 1
Splitting Sums
A lower bound for
n
å k ³
k = 1 |
n
å 1 = n
k = 1 |
is
n
å k =
k = 1 |
n/2
å k +
k = 1 |
n
å k ³
k = n/2 + 1 |
n/2
å 0 +
k = 1 |
n
å n/2 ³
k = n/2 +1 |
0 + (n/2)2 = W (n2/4) |
ignoring initial terms
n
å ak
=
k = 0 |
k0-1
å ak +
k = 0 |
n
å ak =
O(1) +
k = k0 |
n
å ak
k = k0 |
¥
å k2 / 2k =
k = 0 |
2
å k2 / 2k +
k = 0 |
¥
å k2 / 2k
£ O (1) +
k = 3 |
¥
9/8 å (8/9)k
k = 0 |
((k + 1)2 ) / 2k+1 * 2k / k2 = ((k + 1)2 ) / 2k2 £ 8/9
with k £ 3 Þ O (1)
| Hn =
|
n
å 1/k £
k = 0 |
ë lg nû
å
i = 0 |
2i- 1
å 1/ ( 2i + j )
j = 0 |
| £
|
ë lg nû
å
i = 0 |
2i- 1
å 1 / 2i £
j = 0 |
ë lg nû
å 1 = lg n + 1
i = 0 |
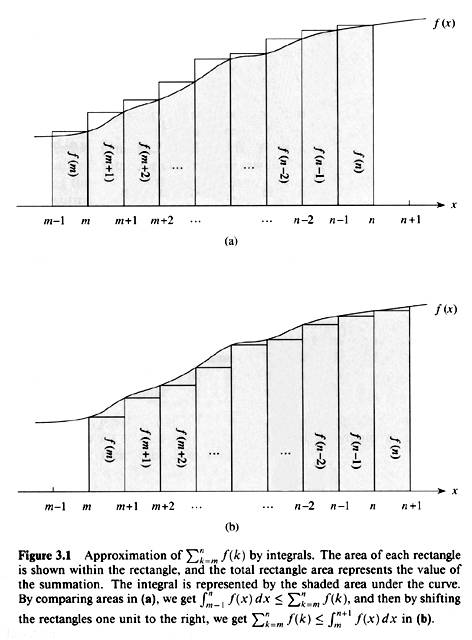
Approximation by integrals
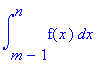 |
n
£ å f (k)
£
k = m |
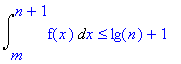 |
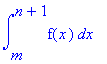 |
n
£ å f (k) £
k = m |
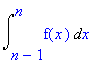 |
n
å 1 / k ³
k = 1 |
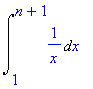 |
= ln ( n + 1 ) |
n
å 1 / k £
k = 2 |
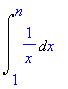 |
= ln n |
n
å 1 / k £
k = 1 |
ln n + 1 |
|
|







