Depth-First Search

Go deeper whenever you can! Edges are explored out from the most recently discovered vertices, v, with outgoing edges. When all of v's edges have been explored you "back track" to explore edges leaving the vertex where v was discovered. If there are undiscovered vertices, you restart from there. When v is discovered while scanning Adj[u]: p[v] = u (like BFS) But the predecessor sub graph (not a tree) is G_p  = ( V, E_p  ) E_p  = { ( p[v], v ):  v Î V and  p[v] ¹ nil }

Several trees: G_p  called a depth-first forest made up of many d-f trees (several  starting points.) Vertices are colored as in BFS. Depth-first search time stamps each vertex.

d[v] : when grayed

f[v] : when blackened

1 £ d[v], f[v] £ 2 | V | as one d and one f event for each vertex. d[v] < f[u] white, d[v] gray, f[u] black. Ordering of the events is the same, locally, but different globally with BFS.

DFS ( G )

1. for each vertex u Î V[G]

2.    do color[u] ¬ white

3.       p[u] ¬ nil  // initialization

4. time ¬ 0

5. for each vertex u Π V[G]

6.    do if color[u] = white

7.       then DFS-Visit (u)   // start from each white

DFS-Visit (u)

1. color[u] ¬ gray  // white vertex has just been discovered

2. d[u] ¬ time ¬ time + 1

3. for each v Î Adj[u] // explore edge ( u, v )

4.    do if color[v] = white

5.       then p[v] ¬ u

6.          DFS-Visit (v)

7. color[u] ¬ black   // Blackened u; it is finished

8. f[u] ¬ time ¬ time + 1

Note: no Q, recursion instead. d[u] is enqueuing, f[u] is dequeuing.

Running time DFS  O ( | V | ).  DFS-Visit S | Adj[u] |. Overall O ( | V | + | E | ) same as BFS.

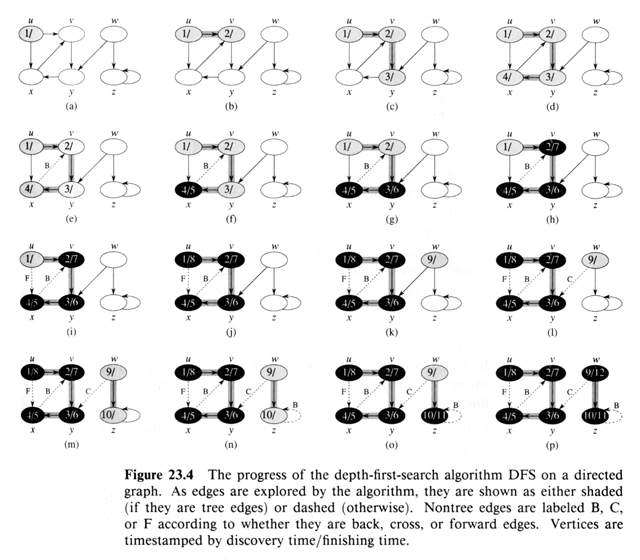
Properties of DFS:

1. G_p , DFS predecessor sub graph is a "forest" of trees and exactly represents the calls to DFS-Visit, which is recursive.

2. The discovery time d[u] and finish time f[u] have the parenthesis property

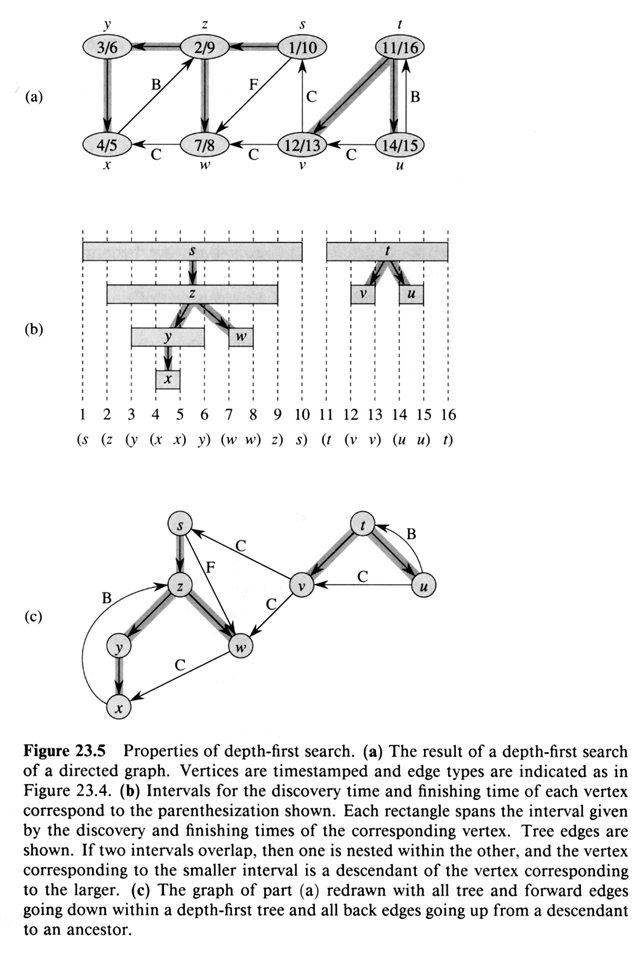
Note: the expression in figure b is well formed since the p's are properly nested.

Parenthesis Theorem: 

In a DFS of G for u, v Î V [ d[u], f[u] ] = I₁ V [ d[v], f[v] ] = I₂ . Either:

1. I₁ Ç I₂  = Æ

2. I₁ Ì I₂ or

3. I₂ Ì I₁

(proof is from the recursive nature of DFS-Visit.)

Nesting of Descendant's Intervals: 

If v is a proper descendant of u in a DF Forest (same tree) iff d[u] < d[v] < f[v] < f[u].

 White-path Theorem:

 In a DF Forest of G = ( V, E ) v is a descendant of u Û at d[u] (when u is discovered) v can be reached ffrom u along a path that is all white.

Proof: AT d[u], v hasn't been discovered, and so all is white in between.

Edges in DFS:

Tree Edges: edges in G_p  ( u, v ) if v was discovered first via ( u, v ).

Back Edges: ( u, v ) v is an ancestor of u (also self loops).

Forward Edges:  ( u, v ) v a descendant but ( u, v ) not a Tree.

Cross Edges: All others

Can modify DFS to categorize the edges by color of vertex when first encountered:

white: tree

gray: back

black: forward

Last Theorem: In a DFS of G, undirected, every edge of G is either a tree or back edge. Proof: See book.