Q, O, W and Asymptotic notation in equations

W notation: asymptotic lower bound

W g ((n))  = { f (n) : $ constants c₁, n₀ > 0   '  0  £  c₁ g (n)   £  f (n) " n   ³  n₀

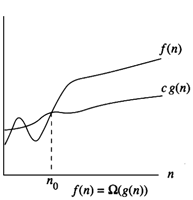from Cormen figure 2.1

• O ( g (n) ) is the top piece of bread

• W ( g (n) ) is the bottom piece of break

• in the Q ( g (n) ) sandwich

f (n) = Q ( g (n) )  Û f (n) = O ( g (n) ) and f (n)  = W ( g (n) )

Thus "Big - Oh" is a bound on worst case, W is a bound (from below) on best case. For example in the case of insertion sort, for all inputs n:

T (n) = O (n²)
         = W (n)

"Running time is W ( g (n) )" means that no matter what input the running time is at least c * g (n) for large n.

Anonymous functions

Recall that for Merge-Sort:

T (n) = 2 T (n/2) + Q ( n ) :: the Q ( n ) here is an anonymous function

the details are not wanted or needed, given an equation:

 2 n² + 3 n + 1 :: we write  2 n² + Q ( n ) or Q ( n ) + some anonymous function of the order of theta of n.

 In this example 2 n² + 3 n + 1 = 2 n² + Q ( n ) = Q ( n² )  as 3 n + 1 is an anonymous function of n, and Q ( n² ) overwhelms Q ( n ) as values of n become large.

"Little-Oh" Notation"

o ( g (n)) = { f (n) ::  " c > 0 , $  n₀ > 0  '  0  £  f (n)  £  c g (n) " n   ³  n₀

The big difference is for all c, thus this is and upper bound that is not tight. It also means that:

w Notation  (w  is to o as W is to O )

w ( g (n)) = { f (n) ::  " c > 0 , $  n₀ > 0  '  0  £  c g (n)  £  f (n) " n   ³  n₀

hence w f (n) = ( g (n) )  Û  g (n) = o ( f (n) )