Q - Notation:

For a given function g (n) :
Q (g(n)) = { f (n) : $ constants c₁, c₂, n₀  ³  0  £  c₁ g (n)   £  f (n) £  c₂ g (n)  " n   ³  n₀

This means: At some point F (n) is sandwiched between c₁ g (n) and c₂ g (n) :

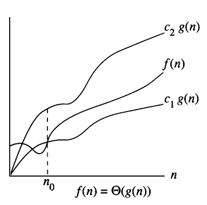from Cormen figure 2.1

Q ( g (n) ) is a set of functions, yet we write " f (n) = Q ( g (n) )" to mean that f (n) Î Q ( g (n) ) We use set notation because of sandwiching for  n   ³    f (n) is equal to g (n) to within a constant factor, therefore g (n) is an asymptotically tight bound for f (n).

Note: The definition requires all f (n) Î Q ( g (n) ) to be asymptotically non-negative. This means that g (n) must be as well.

Example Problem:

Show that f (n) = n²/2 - 3n  Π Q ( n² )  -- we must find n₀, c₁,c₂ for  this definition that fit the equation:

c₁ n²   £  n²/2 - 3n  £  c₂ n²    " n   ³  n₀

c₁   £  1/2 - 3/n  £  c₂  by dividing by  n²

 If n ³  1 then 1/2 - 3/n £  1/2  by making c₂ equal to 1/2

1/2 - 3/n  ³  1/14 when n  ³ 7   ( 1/2 - 3/n = 0 when n = 6 )

So c₁ = 1/14, c₂   = 1/2,  n₀  =  7

Note: other constants work, but we FOUND a set that does.

Consider the contradiction  6 n³  ¹  Q ( n² ) Suppose this were true:

6 n³  £  c₂ n²   " n   ³  n₀

6   £  c₂/n  " n   ³  n₀ then n  £  c₂/6

A note on condensing expressions:  f (n) = an²  + bn + c is Q ( n² ), in fact:

(proofs are in the text book)