Huffman Codes

Methods for compressing data. The Huffman greedy algorithm uses character frequencies.

File with 100000 characters:

Frequency	Fixed-Length Codeword	Variable-Length Codeword
a   45000	000	0
b   13000	001	101
c    12000	010	100
d    16000	011	111
e     9000	100	1101
f    15000	101	1100

3 bits per character ® 300000 bits without "coding" Using a variable-length code: Short code for frequent characters, long code for rare characters.

Character	Frequency	Bits
a	45000	1
b	13000	3
c	12000	3
d	16000	3
e	9000	4
f	5000	4

A total of 224,000 bits, much more compact than the original 300,000 bits. How do we choose the variable length code words?

Fixed Codes:

Code words are not prefixes of other code words. Can show that optimal compression can always be achieved with a prefix code, so only consider them.

a	b	c
0	101	100

a b c = 0 101 100 = 0101100 so

	aaa	b	e
0001011101   =	000	101	1101

binary tee whose leaves are the code words is a convenient tool to aid coding.

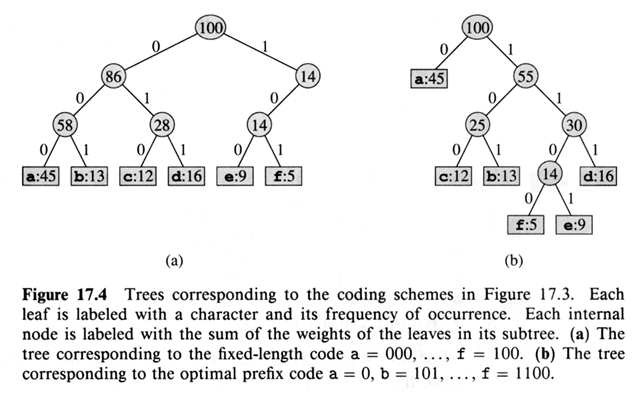
An optimal code for a file is always represented as a full binary tree. Full means every non-leaf child has two children. Note: Fixed-length code tree doesn't. C: Alphabet ® |C| leaves |C| - 1 interval.

B (T) =

å c Î C  f (c) dt (c)

where f(c) is the frequency of c and d_t is the level down the tree (bits required) of c.

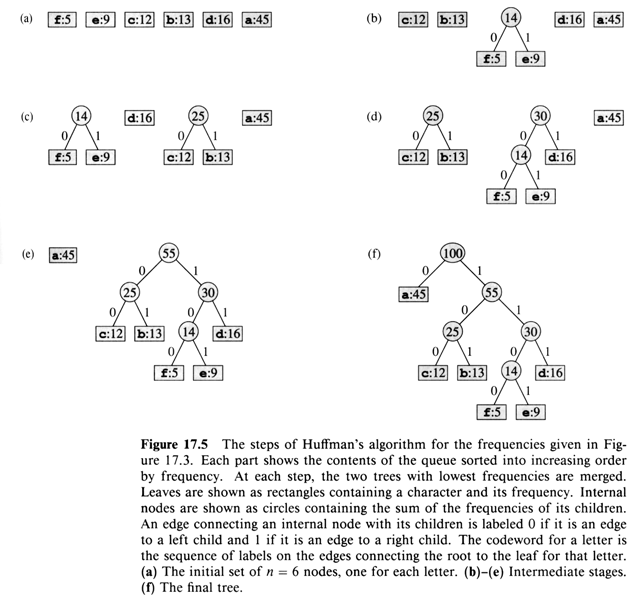
Cost of the T tree. Huffman came up with a greedy algorithm. Q: priority queue keyed on f implemented via a heap. Take two least frequent objects and merge them together.

Huffman (C)

1. n ¬ |C|
2. Q ¬ C
3. for i ¬ 1 to n - 1
4.    do z ¬ Allocate-Node ()
5.       x left[z] ¬ Extract-Min (Q) // least frequent
6.       y right[z] ¬ Extract-Min (Q) // next least
7.       f[z] ¬ f[x] + f[y] // update frequency
8.       Insert ( Q, z )
9. return Extract-Min (Q)

merge into z

Why?

1. Want a full binary tree
2. Want least frequent objects on the bottom

What happens if x and y are replaced in Q with their merged values?

Running Time: Q into heap = O (n), n = |C|, n times through loop, min extract O ( lg n ) so O ( n lg n )

Lemma: Let x and y be in C and have the lowest frequencies. Then $ optimal prefix code where x and y have the same length and their prefix codes differ in the last bit. Why:

1. Must be on the bottom (least frequent)
2. Full tree, so they must be siblings, and so differ in one bit.

See the book for full proof.

Lemma: Let T be a full binary tree representing an optimal prefix code over C. x, y are sibling leaves in T with f (x), f (y) and z is their parent. Then T' = T - { x, y } with f (z) = f (x) + f (y) is also a representation of an optimal prefix code.

Proof: B (T) in terms of B (T') " c Î C - { x, Y } d_T (c) = d_T' (c) so

f (c) d_T (c) =  f (c) d_T' (c)

d_T (x) = d_T (y) = 1 + d_T' (z)

f (x) d_T (x) + f (y) d_T (y) = ( f (x) + f (y) ) ( 1 + d_T' (z)  )

= f (z)  d_T' (z) + f (x) + f (y)

B (T) = B (T') + f (x) + f (y)

if T' is non-optimal then T", optimal and can get B (T) = B (T") + f (x) + f (y) contradicting T's optimality. T' optimal for C' = C - { x, y }