Greedy Algorithms

When doing an optimization there are often may steps taken. DP may often be overkill when a simpler more efficient "greedy algorithm" would do. A greedy algorithm makes the best choice at that moment, hoping this will produce the optimum in the long run.

An activity selection problem:

Optimal scheduling of a resource among several competing activities (scheduling rehearsal times in a music studio)

Problem setup: S = {1, 2, ..., n} a set of n proposed activities. Each activity has s_i a start time, and F_i a finish time s_i £ f_i. If activity i is selected, the resource is occupied in the interval [s_i ,  f_i). We say i and j are compatible activities if either or i.e. that

[s_i ,  f_i) Ç [s_j ,  f_j) = Æ

The activity-select problem is to select a maximal sized subset of mutually compatible activities. Note: Here we maximize the number of activities selected, but if the profit were proportional to s_i -  f_i , this will not maximize profit (renting out a hall.)

Greedy Algorithm:

Assume that f₁ £ f₂  £  ...  £  f_n 

Greedy-Activity-Selector ( s, f )

1. n ¬ length [s]

2. A ¬ { 1 }

3. j ¬ 1

4. for i ¬ 2 to n

5.    do if s_i ³  f_i

6.       then A ¬ A È{ i }

7.          j ¬ i

8. return A

  

 

The algorithm starts with { 1 } and checks to see which can be added after 1, updating the golbal "finishing time" and comparing with each start time. Note: f_j is always the global "finishing time" of previously selected activities.

Running Time:

1. sorting n activities by f_j O ( n lg n )

2. Greeed-Activity-Selector Q ( n )

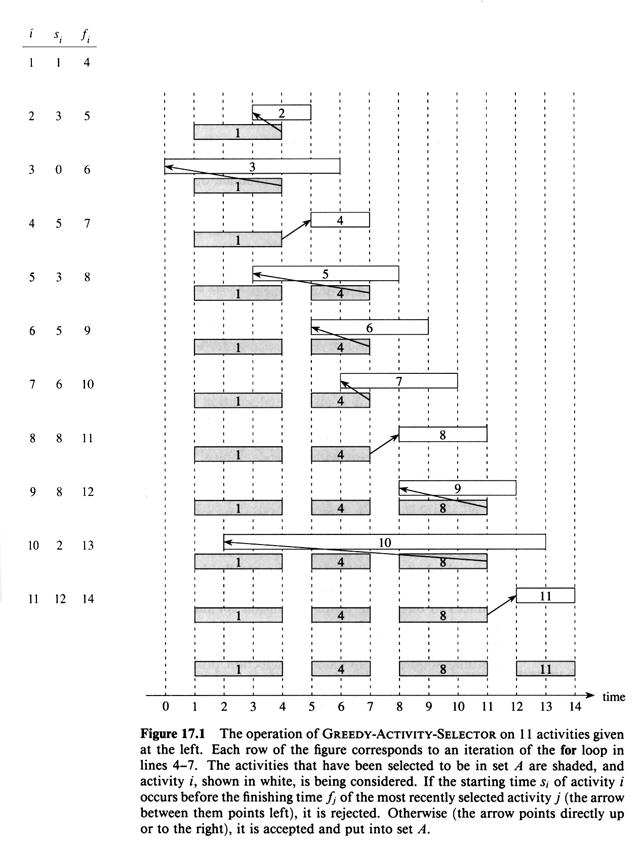
The activity picked is always the first that is compatible. Greedy algorithms do not always produce optimal solutions.

Theorem 17.1:

 Algorithm Greedy-Activity-Selector produces solutions of maximal size for the activities-selection problem.

Proof:

Let S = { 1, 2, ... n }, are sorted 1 has the earliest finishing time. We wish to show there is an optimal solution that begins with activity 1. Suppose A £ S is an optimal solution and the first activity is k ¹ 1. We want to show that optimal B exists that begins with 1. Let B =  A - { k }È { 1 }. Since f_i £  f_k all activities in B are disjoint and |B| = |A|,  so it is optimal. Now, when the greedy choice of 1 is made, the problem reduces to activity selection on { 2, 3, ... n }, which are all compatible with 1. So if A is the greedy optimum to S, the Aⁱ = A - { 1 }is the greedy optimum to S = { i Î S, s_i ³  f_i}. Why, if we could find and optimal Bⁱ to Sⁱ with |Bⁱ| > |Aⁱ|, then Bⁱ È { 1 } would be optimal for S and |B| > |A| which contradicts that A is optimal for S.

Thus after each greedy choice we are left with essentially the same optimization problem. By induction the greedy algorithm always finds a minimum, one activity at a time.