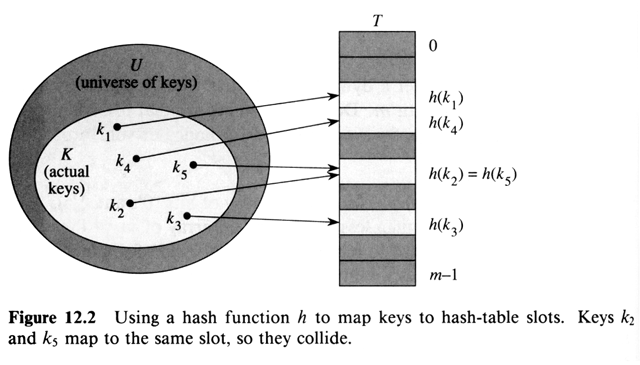
Hash Tables
What if |U| is large, and the set of Keys actually stored,
K, is small ?
|U| >> |K|
Can build a hash table of size Q (
|K| ) and can reduce searching to O (1), on average. With a hash
function h (k) we store x with k = key[x] in h (k). h: U ®
K, since |U| >> |K| we expect collisions.
We say k hashes to slot h (k) and h (k) is the hash
value of key k.
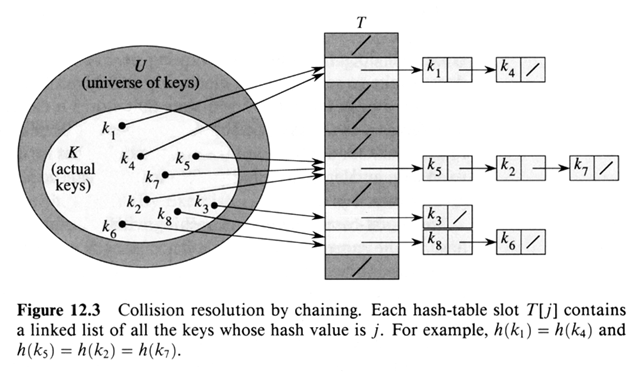
Chained-Hash-Insert ( T, x ), insert x at the head of list
T[h(key[x])] O (r), r = number of elements in T [ h (k) ]
Chained-Hash-Search ( T, x ), search for an element with key
k in list T[h(k)] O (r)
Chained-Hash-Delete ( T, x ), delete x from the list
T[h(key[x])] O (1)
Clearly, collisions are minimized if h is a
"randomizing" function. Given T, a hash table, with m slots
storing n elements.
a = n/m is the load factor (
often consider a fixed as n, m ®
¥ )
Worst-case behavior of hashing with chaining is Q
( n ) + time to compute h (k). This occurs when all n elements hash
to a single slot.
Assume this doesn't happen: Simple Uniform Hashing: a
given Key, k, is equally likely to hash to any of the m slots (values of h
(k)).
Assume h (k) cand be computed in O (1). Thus
searching for an element with key k is proportional to T[h(k)]'s length. We
must analyze this (T[h(k)]'s length) it two cases: search unsuccessful,
and search successful. (Assume simple uniform hashing.)
Unsuccessful: In T with collision resolution through
chiaining, search time is Q ( 1+a
), in the average case.
Proof: Any key, k, is equally likely to hash into ANY
of the m slots. Thus the time to unsuccessfully search is the time to search
through one of the m lists. Average length = n/m = a. With h (k) computation
costing O (1) plus O (a) for
searching, we get O ( 1+a ).
Successful: A successful search in a hash table with
chaining takes time Q ( 1+a
). Assume Chained-Hash-Insert adds new elements to the end of the list. The
time to search for element with key k is one more (the successful element)
than searched for when inserting that element. The length of the list to
insert the ith element is ( i - 1 ) / m , so expected elements
examined in successful search:
| 1 / n |
n
å
i = 1
|
(1 + ( i - 1) / m ) |
|
| = 1 + 1/ n m |
|
| = 1 + 1/ n m |
|
| = 1 + ( n ( n-1 )) / 2 n m |
|
| = 1 + n/ 2 m - 1 / 2 m |
|
| = 1 + a/2 - 1 / 2 m |
|
Running time = 2 + a/2 - 1 / 2 m
= Q ( 1+a )
Note: if a = n/m = O (1) ,
n » m, then all run (expected) in O (1) .
Why do you need to hash?
Discrete log problem (Diffie-Helman) Let a generate a
group G, thus for any element e Î G
e = ai for some i
0 £ i < |G|
(An example is G = integers mod p, a is a primitive root mod
p.)
Discrete log problem in G: Given a and e find i. A
general solution to this problem is the giant-step / baby-step algorithm:
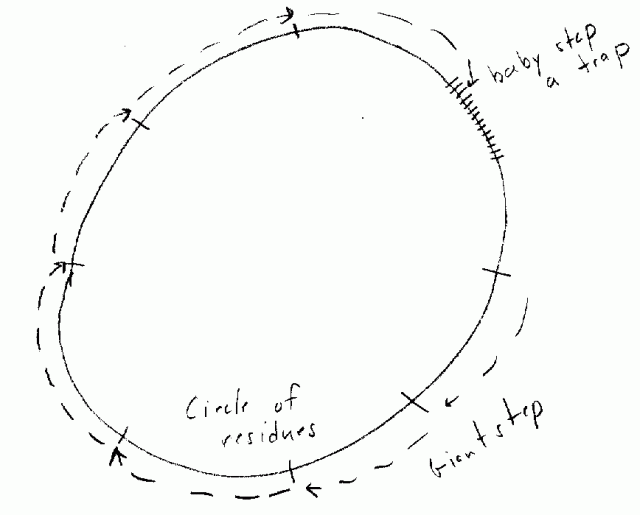
Building a Kangaroo trap for solving the discrete log problem.
Each giant-step see if you land in the "baby-step"
region. Need O (Ö |G|)steps to do this,
on average. This is the "Birthday Paradox". |G| = 264 Ö
|G|) = 232, must hash. |







