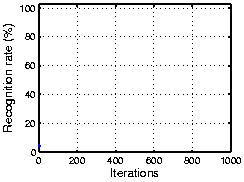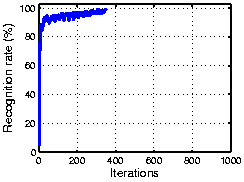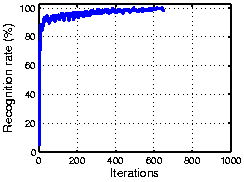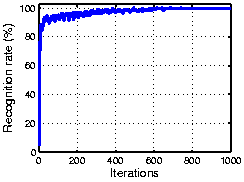
Here the initial representation is computed using an ICA algorithm.

• Toy example.
  To demonstrate the effectivess of the OCA technique, here we use a toy example. Two classes ('+' and 'o') are shown in the following image.

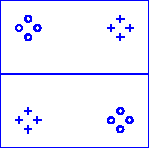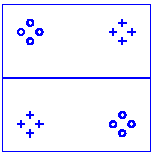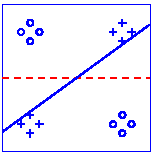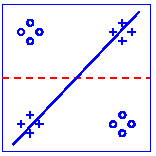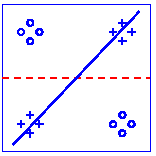
  A toy dataset of two classes with eight points each	1-d linear projection given by PCA/ICA/FDA

  In this case, one can easily show that for recognition, 1-d projection given by a typical PCA/FDA/ICA algorithm is given by the image on the right. The recognition performance (in the nearest neighbor sense) is poor. By using the proposed technique, we can find an optimal solution. The following figures show the temporal evolution of the optimization process. The plot on the left shows the temporal evolution of the linear representation during the optimization process and the one on the right shows the distance of the linear representation from the initial one; note that even though the recognition process reached 100% and the optimization continues to have a representation with better generalization. To visualize the linear bases given by the optimization process, the following figure shows the corresponding 1-d projection during the temporal evolution. The corresponding linear representation is imposed on the image. Note here the red dashed line is the initial basis
• We have applied OCA on different kinds of datasets, including face recognition and object recognition. We obtained consistently successful recognition performance in all cases.

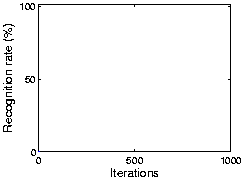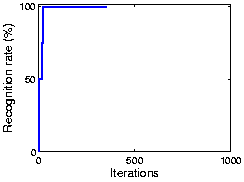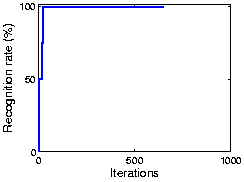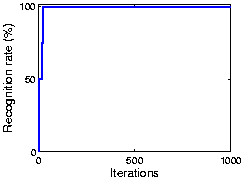
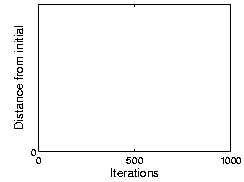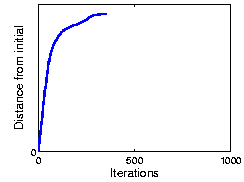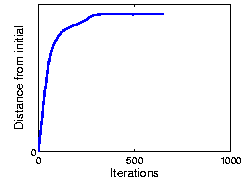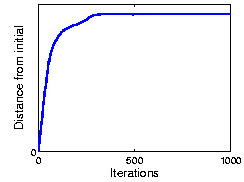
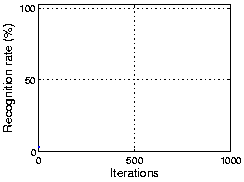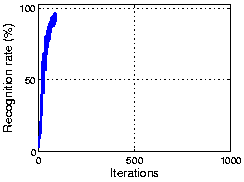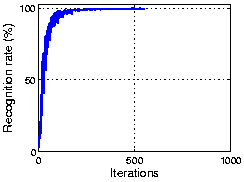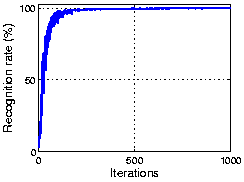
  The following figure shows the result using the ORL face dataset. As the plot shows, OCA achieves 100% recognization. Here the initial performance is given by an ICA algorithm.

  

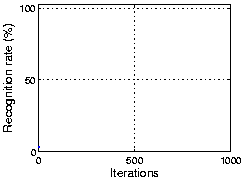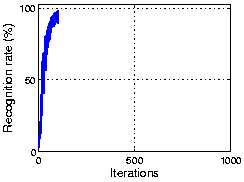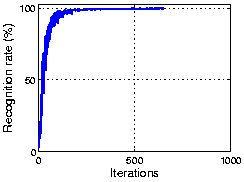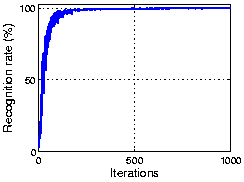
  The following figure shows the result using part of COIL 3D object dataset. As the plot shows, OCA achieves 100% recognization. Here the initial performance is given by an ICA algorithm.

  

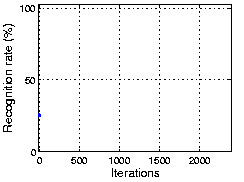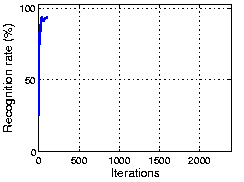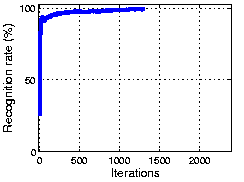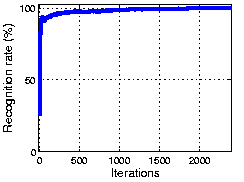
  The following figure shows the result using part of the CMU PIE dataset. As the plot shows, OCA achieves 100% recognization. Here the initial performance is given by an ICA algorithm.

  

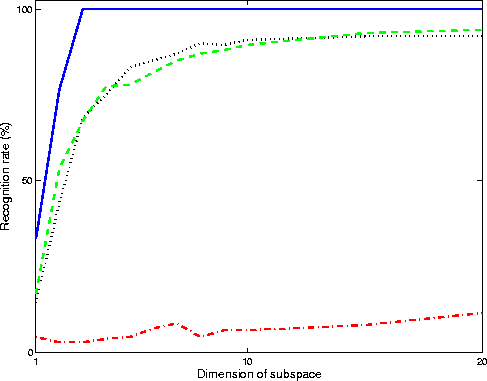
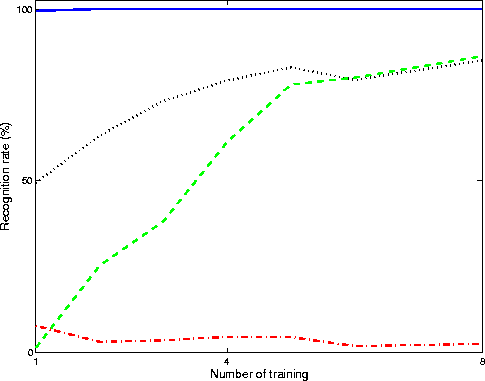
• The following figure compares OCA with other popular choices such as PCA, FDA, and ICA with respect to the number of subspaces on the ORL face dataset. The plots clearly show the effectiveness of OCA. Here the solid blue plot is the performance achieved by OCA with respect to the dimension of subspace; red dash-dotted ICA; green dashed FDA; black dotted plot PCA.

  
  We aslo compare the performance with respect to the number of training images for a subspace of dimension 5. The following figure shows the results. As in the previous figure, the solid blue plot is the performance achieved by OCA with respect to the number of training images; red dash-dotted ICA; green dashed FDA; black dotted plot PCA.

References

1. X. Liu, A. Srivastava, and Kyle Gallivan, ``Optimal linear representations of images for object recognition,'' IEEE Transactions on Pattern Recognition and Machine Intelligence, vol. 26, no. 5, pp. 662--666, 2004.
2. X. Liu, A. Srivastava, and K. Gallivan, ``Optimal linear representations of images for object recognition,'' In the Proceedings of the International Conference on Computer Vision and Pattern Recognition, vol. I, pp. 229--234, 2003.
3. Q. Zhang and X. Liu, ``Kernel optimal component analysis,'' In the Proceedings of the IEEE Workshop on Learning in Computer Vision and Pattern Recognition, 2004.
4. W. Mio, Q. Zhang and X. Liu, ``Nonlinearity and optimal component analysis,'' In the Proceedings of the International Conference on Neural Networks, 2005.
5. Q. Zhang and X. Liu, ``Hierarchical learning of optimal linear representations,'' In the Proceedings of the International Joint Conference on Neural Networks, 2003.

Acknowledgement

Disclaimer