Specifying Syntax: Regular expressions and context-free grammars

• Regular expressions are formed by the use of three mechanisms

  • Concatenation
  • Alternation
  • Repetition (aka Kleene closure)

Specifying Syntax: Regular expressions and context-free grammars

• A context-free grammar adds one more mechanism: recursion

Tokens and regular expressions

• Tokens are the basic lexical unit for a programming language

  • In C for instance, "while" and "return" are tokens, as are identifier names, such as "printf", as well as operators and parentheses
  • (N.B. - parentheses are bizarrely called "punctuators" in the C family of languages, which is neologistic at best since previously "punctuator" merely referred to a person doing punctuation.)

Tokens and regular expressions

• Tokens are specified by regular expressions

Tokens and regular expressions

• Consider the regular set for numeric expressions given in the text on page 44:

$$number \rightarrow integer | real $$ $$integer \rightarrow digit\ digit* $$ $$real \rightarrow\ integer\ exponent\ |\ decimal\ (\ exponent\ |\ \epsilon\ )$$ $$decimal \rightarrow\ digit*\ (\ .\ digit\ |\ digit\ .\ )\ digit*$$ $$exponent \rightarrow\ (\ e\ |\ E\ )\ (\ +\ |\ -\ |\ \epsilon\ )\ integer$$ $$digit \rightarrow\ 1\ |\ 2\ |\ 3\ |\ 4\ |\ 5\ |\ 6\ |\ 7\ |\ 8\ |\ 9\ |\ 0$$

Tokens and regular expressions

• Notice that there is no recursion in the previous set of rules. Were there even an indirect recursion, this would not describe regular expression but instead a context-free grammar.

Tokens and regular expressions

• You can consider the previous set of rules as a generator for the initial token "number"; starting with the first rule, you can expand each.

• For instance,

$$number \Rightarrow integer \Rightarrow digit\ digit*$$ $$\ \Rightarrow 1\ digit* \Rightarrow 1\ 3\ digit* \Rightarrow 1\ 3$$

Character sets and formatting issues

• Some languages ignore case (most Basics, for instance); many impose rules about the case of keywords / reserved words / built-ins; others use case to imply semantic content (Prolog and Go, for instance)

• Some languages support more than just ASCII

Character sets and formatting issues

• Most languages are free format, with whitespace only providing separation, not semantics

• However, line breaks are given some significance in some languages, such as Python and Haskell

• There are even modern languages like Python and Haskell that do care about indentation to one or degree or another

Character sets and formatting issues

• In contrast, there were languages that had quite rigid rules about line formatting (Fortran and RPG come to mind here.)

Other applications of regular expressions

• Of course, regular expressions are widely used in scripting languages (Perl's "regular expressions" in particular have had wide acceptance in other languages, and are generally available in the Linux environment via libpcre)
• What Perl calls a "regular expression" is actually more than just a regular expression, and indeed for some time the Perl developers had planned to rename them to just "rules" in Perl 6 but have backed off of that decision

Other applications of regular expressions

• One of the most popular extensions to regular expression syntax is the ability to, while matching, specify portions of the match.

"a4b6" =~ /a([0-9])b([0-9])/

Other applications of regular expressions

• For instance, the previous Perl "regular expression", when applied against the string "a4b6" would set the variable $1 to "4" and the variable $2 to "6":

$ perl
"a4b6" =~ /a([0-9])b([0-9])/ ;
print $1 . "\n";
print $2 . "\n";
4
6

Context-free grammars in Backus-Naur Form (BNF)

• While regular expressions are ideal for identifying individual tokens, adding recursion to the mix means that we can now recognize "context-free grammars". Context-free grammars have the advantage of allowing us to specify more flexible structure than mere regular expressions.

• Each rule is called a production. The symbols that appear on the left-hand side of a production rule are called non-terminals.

Context-free grammars in Backus-Naur Form (BNF)

• Since we will use Lemon for generating parsers, it is a particularly good idea to note the discussion on page 47 about the equivalent meaning of the single production

$$op \rightarrow +\ |\ -\ |\ *\ |\ /$$

Context-free grammars in Backus-Naur Form (BNF)

• and the set

$$op \rightarrow +$$ $$op \rightarrow -$$ $$op \rightarrow *$$ $$op \rightarrow /$$

Derivations and parse trees

• Using the grammar

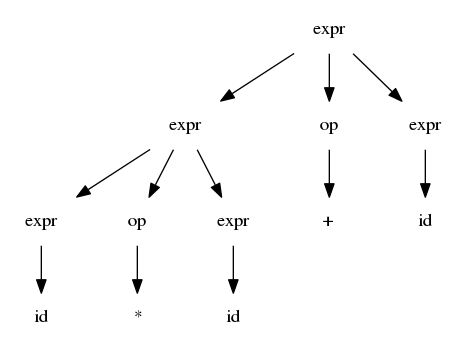
$$expr \rightarrow id\ |\ number\ |\ -\ |\ expr\ |\ (\ expr\ )$$ $$op \rightarrow +\ |\ -\ |\ *\ |\ /$$

• We can derive

$$expr \Rightarrow expr\ op\ expr\ \Rightarrow expr op id \Rightarrow expr\ +\ id$$ $$\Rightarrow expr\ op\ expr\ +\ id\ \Rightarrow expr\ op\ id\ +\ id\ \Rightarrow expr\ *\ id\ +\ id$$ $$\Rightarrow id\ *\ id\ +\ id$$

Derivations and parse trees

• Or the can be written in a summary fashion as

$$expr \Rightarrow^{\star} id\ *\ id\ +\ id$$

Derivations and parse trees

Derivations and parse trees

• This grammar is ambiguous, but on page 50, there is an equivalent grammar given that is not:

$$expr \rightarrow term\ |\ expr\ addop\ term$$ $$term \rightarrow factor\ |\ term\ multop\ factor$$ $$factor \rightarrow id\ |\ number\ |\ -\ factor\ |\ (\ expr\ )$$ $$addop \rightarrow\ +\ |\ -$$ $$multop \rightarrow\ *\ |\ /$$

Derivations and parse trees

• What's the difference in the two previous grammars? Why is one ambiguous and the other not?

Scanning

• Usually, scanning is the fast, easy part of syntax analysis; it is usually linear or very close to it; importantly, it removes the detritus of comments and preserves semantically significant strings such as identifiers. (Note the weasel word "usually"!)

• Examples of scanner generators are lex, flex, and re2c.

Scanning

• However, since scanning is generally quite simple, it is often done ad hoc with custom code (for instance, see figure 2.5 in the text, or here.)

Scanning and automata

• The most general type of automaton is a non-deterministic finite automaton (NFA, sometimes NDFA) based on the 5-tuple

$$(S,\Sigma,Move(),S0,Final)$$

where S is the set of all states in the NFA, Sigma is the set of input symbols, Move is the transition() function that maps a state/symbol pair to sets of states, S0 is the initial state, and Final is the set of accepting/final states. (See section 3.6 of the Dragon Book).

Scanning and automata

• An NFA is entirely general since it allows both:

  • From a given state, an NFA allows multiple exits by a single input
  • From a given state, an NFA allows an epsilon (null) transition to another state

Scanning and automata

• A deterministic finite automaton is a type of NFA where

  • From a given state, a DFA allows only one exit by a single input
  • From a given state, a DFA does not allow an epsilon (null) transition to another state

• Both an NFA and a DFA are equivalent in expressive power, and can always be transformed from one to the other.

Generating a finite automaton

• Scanner generators allow us to automatically build a finite automaton. This is done by writing a specification for, say, flex or re2c. Then, typically, the scanner generator will first create an NFA from our specification, and then rewrite that to a DFA. Then it's likely that the generator will then attempt to reduce the number of states in the DFA.

Parsing

• A parser is a language recognizer. We generally break parsers up into two CFG families, LL and LR.

• Parsing has generally the arena for context-free grammars, but other techniques have recently gained quite a bit of attention. Packrat parsing and PEGs have recently become an area of interest since the methodology seems to offer some benefits over CFGs. I imagine the 4th edition, out in November, will cover more on this subject.

Parsing

• LL parsers are top-down parsers, and usually written by hand (good old recursive-descent parsing!)

• LR parsers are bottom-up parsers, and are usually created with a parser generator. (Also see SLR parsing, as referenced in your book on page 70.)

Parsing

• LL stands for "Left-to-right, Left-most derivation"

• LR stands for "Left-to-right, Right-most derivation"

Parsing

• Consider

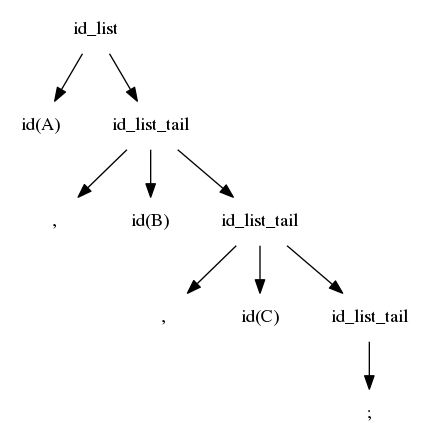
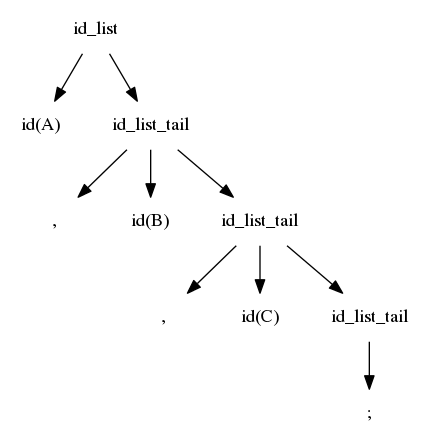
$$idlist \rightarrow id\ idlisttail$$ $$idlisttail \rightarrow ,\ id\ idlisttail$$ $$idlisttail \rightarrow ;$$

• This grammar can parsed either way, either top-down or bottom-up

Parsing A, B, C; with previous grammar, top-down step 1

Parsing A, B, C; with previous grammar, top-down step 2

Parsing A, B, C; with previous grammar, top-down step 3

Parsing A, B, C; with previous grammar, top-down step 4

Bottom-up parsing

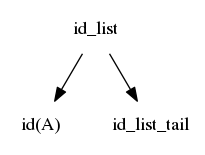
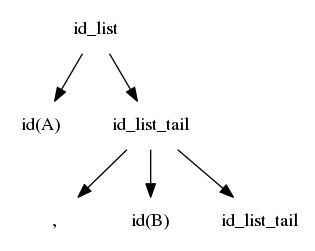
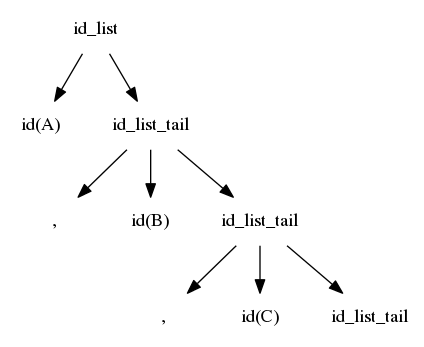
• We reverse the search; we again start at the left, but we are now trying to match from the right

• The first match is when id_list_tail matches ";"

Bottom-up parsing

• The next rule that matches is then:

Bottom-up parsing

• The next rule that matches is then:

Bottom-up parsing

• The next rule that matches is then:

A better bottom-up grammar for lists

• As illustrated in figure 2.14 in the text, the following grammar saves a lot of initial shifting for LR parsing, though at the cost of not being usable via recursive descent:

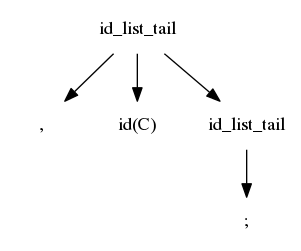
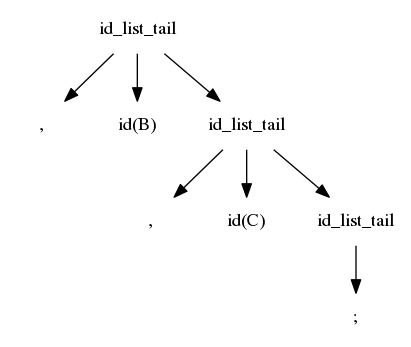
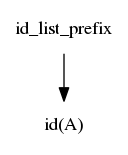
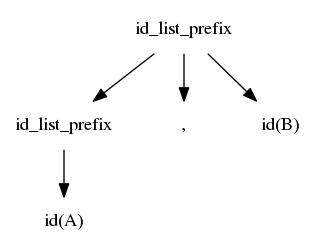
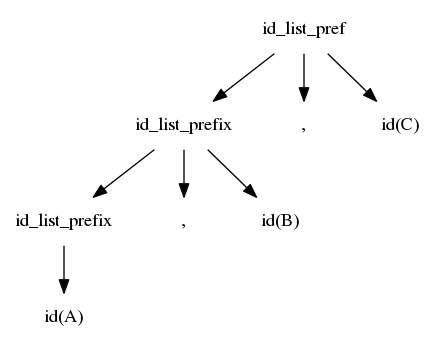
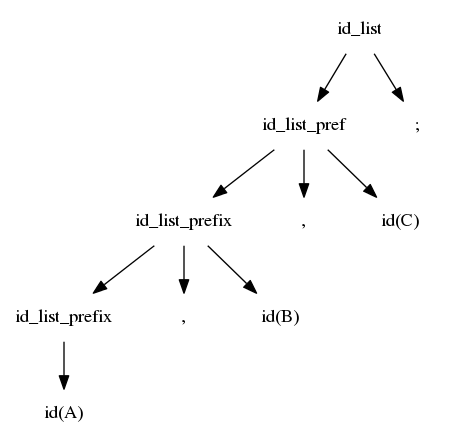
$$idlist \rightarrow idlistprefix\ ;$$ $$idlistprefix \rightarrow idlistprefix\ ,\ id$$ $$idlistprefix \rightarrow id$$

Step 1: Parsing "A, B, C" bottom-up

Step 2: Parsing "A, B, C" bottom-up

Step 3: Parsing "A, B, C" bottom-up

Step 4: Parsing "A, B, C" bottom-up

Recursive descent for the win

• As your book mentions on page 72, GCC is now using a hand-written recursive descent parser rather than bison.

• This is also true for clang.

Figure 2.15: Example LL grammar for simple calculator language

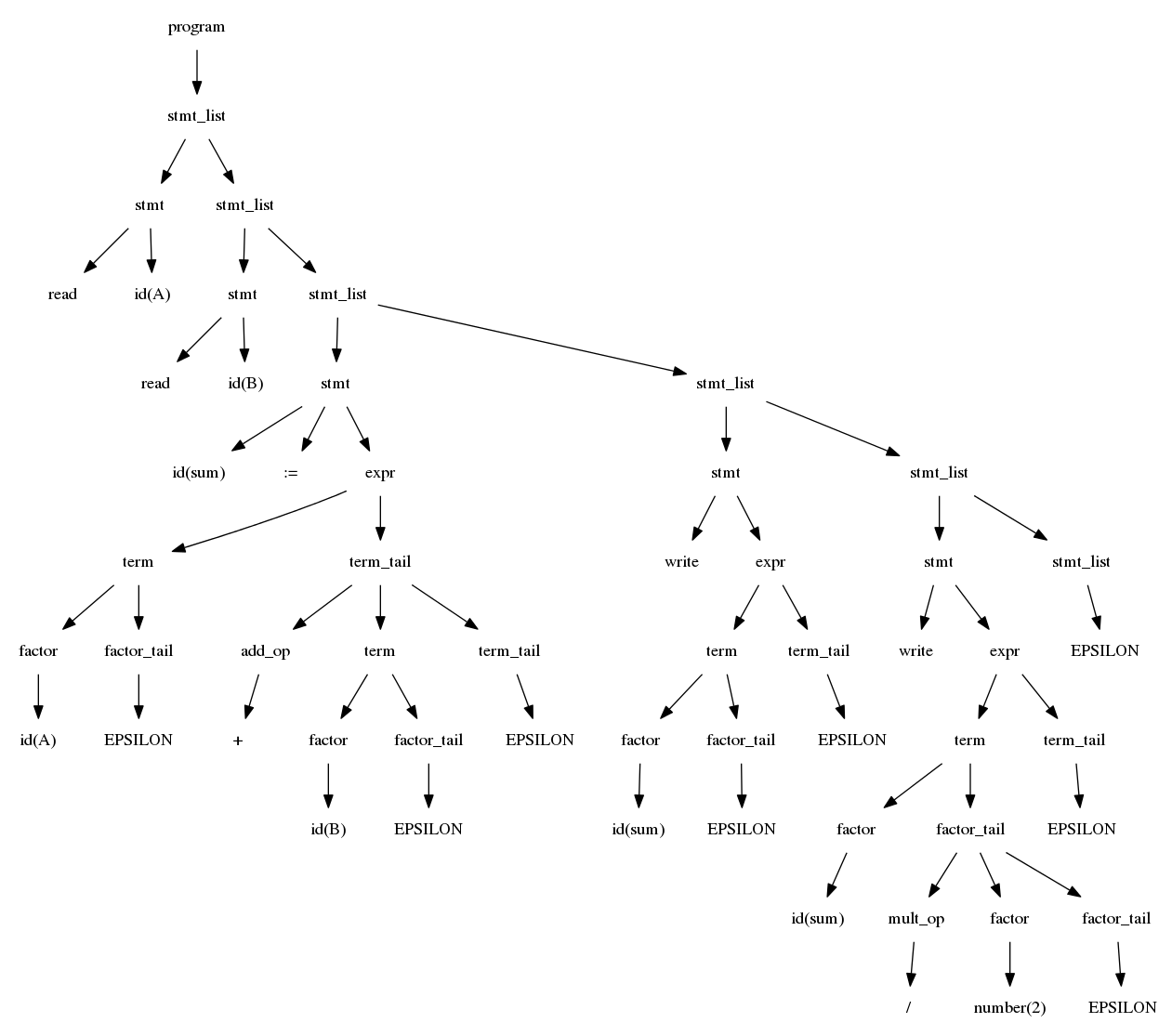
$$program \rightarrow stmtlist EOD$$ $$stmtlist \rightarrow stmt\ stmtlist\ |\ \epsilon$$ $$stmt \rightarrow id\ :=\ expr\ |\ read\ id\ |\ write\ expr$$ $$expr \rightarrow term\ termtail$$ $$termtail \rightarrow addop\ term\ termtail\ |\ \epsilon$$

Figure 2.15 continued: Example LL grammar for simple calculator language

$$term \rightarrow factor\ factortail$$ $$factortail \rightarrow multop\ factor\ factortail\ |\ \epsilon$$ $$factor \rightarrow (\ expr\ )\ |\ id\ |\ number$$ $$addop \rightarrow +\ |\ -$$ $$multop \rightarrow *\ |\ /$$

Example 2.24 "Sum and average program"

 read A
 read B
 sum := A + B
 write sum
 write sum / 2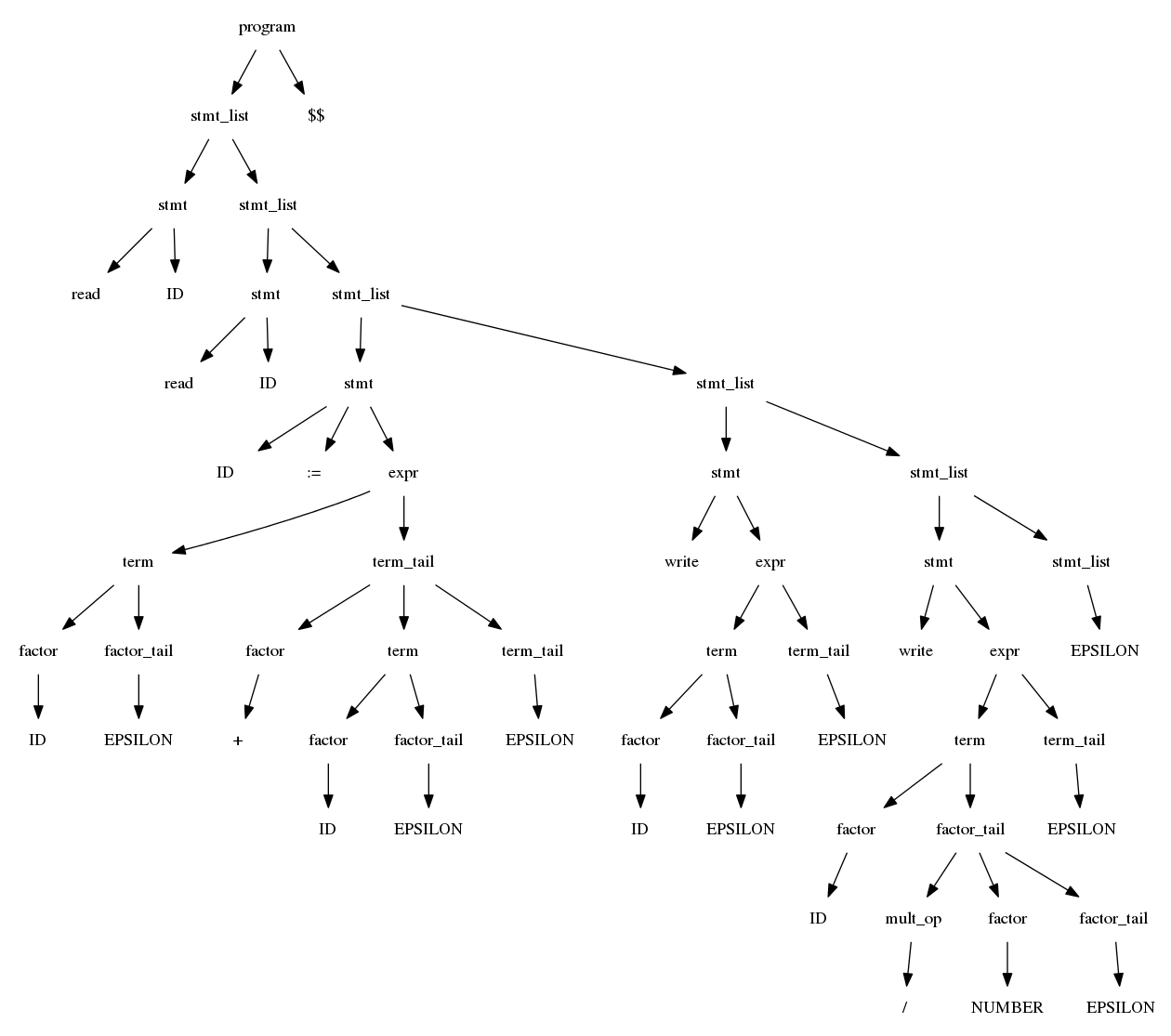

Figure 2.17 Recursive Descent Parse of example 2.24

Figure 2.17 Lemon Parse of example 2.24

Recursive Descent Parser for example 2.24 in C

parser.c

Lemon Parser for example 2.24

grammar.y

Recursive Descent (minimal)

• For each non-terminal, we write one function of the same name
• Each production rule is transformed: each non-terminal is turned into a function call of that non-terminal's function, and each terminal is made into a call for a match
• If a production has alternatives, these alternatives must be distinguished by using the predict set.

Recursive Descent (fully general)

• While figure 2.21 shows that for small examples like the grammar for example 2.24, it is easy to see the first and follow sets, it quickly grows more challenging as grammars grow bigger.

• Your text on pp.79-82 gives definitions and algorithms for computing predict, first, and follow sets.

Disambiguation rules

• As your text says, LL cannot parse everything. The famous Pascal if-then[-else] ambiguity problem is mentioned:

$$stmt \rightarrow if\ condition\ thenclause\ elseclause\ | otherstmt$$ $$thenclause \rightarrow then\ stmt$$ $$elseclause \rightarrow then\ stmt\ |\ \epsilon$$

Disambiguation rules

• What's the solution? The same sort of idea as PEGs and Lemon use: give precedence in order of appearance (i.e., first applicable wins.)

Bottom-up parsing

• Shift and reduce are the fundamental actions in bottom-up parsing

• Page 87: "...a top-down parser's stack contains a list of what the expects to see in the future; a bottom-up parser's stack contains a record of what the parser has already seen in the past."

Bottom-up parsing

The last four lines, the reduction ones, correspond to the derivation

$$idlist \Rightarrow id\ idlisttail \Rightarrow id,\ id\ idlisttail$$ $$\Rightarrow id,\ id,\ id\ idlisttail \Rightarrow id, id, id;$$