Polynomials and the FFT

Preliminaries:

Polynomial A (x) =

n - 1 å j = 0  aj xj

is a polynomial over field 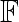. (Example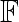s = (reals), 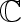(complex), G F (2) (bits))

n is the degree-bound a₀, a₁, ...,a_n-1 are the coefficients.

A (x) is said to have degree k if a_k is the last non zero coefficient, i.e. a_j = 0 for j > k. A polynomial with degree-bound n can have a degree k, 0 £ k £ n - 1. A polynomial with degree k ahs degree-bound n for all n > k.

Sums:

Consider A (x) and B (x), two polynomials for degree-bound n.

A (x) =

n - 1 å j = 0  aj xj

B (x) =

n - 1 å j = 0  bj xj

C (x) is the sum of A (x) and B (x), it has degree-bound n, and C (x) = A (x) + B (x) for all x Î 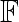. We can write:

 

C (x) =

n - 1 å j = 0  cj xj

where c_j = a_j + b_j

Products:

C (x) is the product of A  (x) and B (x) if C (x) = A (x) B (x) for all x Î 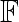and is of degree-bound Z_n - 1. Multiplication is "school book" style:

A (x) = 3x³ + 2x + 1

B (x) = 4x² + 3x - 1

                      3x³ +            2x + 1
                                    4x² + x - 1

---

                     -3x³ +          - 2x - 1
             9x⁴ +             6x² + 3x
12x⁵ +           8x³ +    4x²

---

12x⁵ + 9x⁴ + 5x³ +  10x² +  x - 1

 

C (x) =

Zn - 2 å j = 0  cj xj

, cj =

j å k = 0  ak bj-k

c_j a convolution

 degree (C) = degree (A) + degree (B)

degree-bound (C) = d - b (A) + d - b (B) - 1

                            £ d - b (A) + d - b (B) - 1

We will study fast, recursive, algorithms to compute polynomial products using the discrete Fourier transform ( DFT ) and the fast Fourier transform ( FFT ).