The DFT and FFT

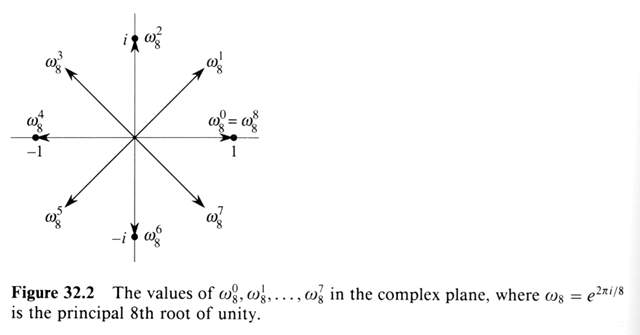
Complex roots of unity ( n^th root ) w ⁿ = 1. There are n, n^th roots of unity.

e^{( 2 p i / n ) k} , k = 0, 1, ..., n-1

recall e^{i u} = cos ( u ) + i sin ( u ) is a point on the complex unit circle. w_n = e^{( 2 p i / n )} is the principal  n^th root of unity.w_n⁰, w_n¹, w_n², ..., w_n^n-1 are the n, n^th roots of unity. They form a group under multiplication ( Z_n, t )

w_nⁿ = w_n⁰ = 1

w_n^j  w_n^k = w_n^{( j+k) ( mod n )}

w_n^-1 = w_n^n-1

Cancellation Lemma:

For all integers n, k ³ 0, d > 0  w_{d n}^{d k} = w_n^k

Proof:

w_{d n}^{d k} = e^{( 2 p i / dn ) dk}   =  e^{( 2 p i / dn ) dk}   = e^{( 2 p i / n ) k} = w_n^k

Corollary for n > 0, even w_n^n/2 = w₂ = -1

Halving Lemma:

If n > 0 is even, then the squares of the n,  n^th roots of unity, are the n/2, n/2^th roots of unity.

(w_n^k )² = e^{( 2 p i / n ) 2k} = e^{( 2 p i / n/2 ) k} = w_n/2^k

We get them twice are

(w_n^k+n/2 )² = w_n^2k+n = w_n^2k w_nⁿ  = w_n^2k  = w_n/2^k

so (w_n^k+n/2 )² =  (w_n^k )² and w_n^k+n/2 = w_n^k w_n^n/2  = - w_n^k

Summation Lemma:

For all n ³ 1, k > 0 with k not divisible by  n we have

n - 1 å j = 0  (wnk )j = 0

Proof:

Note that this a geometric series with x = w_n^k , then recall:

 

n - 1 å j = 0  Zj  =   ( Zn - 1) / ( Z -1 )

here Z = w_n^k  so sum equals ( (w_n^k )ⁿ - 1) / ( (w_n^k ) -1 ).  since k does not divide n (w_n^k ) ¹ 1, but (w_n^k )ⁿ = (w_n^k )ⁿ = (w_nⁿ )^k = 1^k = 1 , so:

n - 1 å j = 0

(wnk )j = 0

The DFT

We want to evaluate A ( x ) =

n - 1 å j = 0

aj xj

the vector y = (y₀, y₁, ...,y_n-1) is called the Discrete Fourier Transform ( DFT ) of the vector a.

 y = DFT_n ( a ) , where n is the size of the vector

The Fast Fourier Transform

Use a divide-and-conquer strategy. Since n is a power-of-two, we can split the A ( x ) polynomial into a polynomial of even and odd powers:

even coefficients: A ^[0] ( x ) = a₀+ a₂ x+ a₄ x²+ ... + a_n-2 x^n/2-1 .

odd coefficients: A^[1] ( x ) = a₁+ a₃ x+ a₅ x²+ ... + a_n-1 x^n/2-1 .

We can get A ( x ) back as follows:

A ( x ) = A^[0] ( x² ) + A ^[1] ( x² )   *

so to evaluate A ( x ) at ( w_n⁰, w_n¹,  ..., w_n^n-1 ) reduces to evaluating A^[0] ( x ) at ( (w_n⁰)², (w_n¹)², ... (w_n^n-1)² ) and  A^[1] ( x )  at the same points, and then combine using *. Note by the halving lemma ( (w_n⁰)², (w_n¹)², ... (w_n^n-1)² ) are the n/2, n/2^throots of unity, twice!! So A ( x) is evaluated at n points A^[0] ( x ) and A^[1] ( x ) are evaluated at n/2 points, but we can recursively continue, dividing by 2 the wole way.

Recursive-FFT ( a )

1. n ¬ length[a]   // n is a power of 2
2. if n = 1
3.    then return a
4. w_n ¬ e^{( 2 p i / n )}
5. w ¬ 1
6. a^[0] ¬ (a₀, a₁, ...,a_n-2)
7. a^[1] ¬ (a₀, a₁, ...,a_n-1)
8. y ^{[0] ¬} Recursive-FFT ( a^[0] )
9. y ^{[1] ¬} Recursive-FFT ( a^[1])
10. for k ¬ 0 to n/2 - 1
11.    do y_k  ¬ y_k^[0] + wy_k ^[1]
12.            y_k+n/2  ¬ y_k^[0] - wy_k ^[1]
13.             w ¬ ww_n
14. return y // y is assumed to be column vector.

This is a divide-and-conquer, halving the size of the FFT each time. Note that the DFT of a single element is y₀ = a₀ w₁⁰ = a₀ , identity. Lines 6 and 7 setup the A^[0] and A^[1] coefficients, lines 8 and 9 are the recursion, lines 10 - 13 do the recombination via *, and lines 4 and 5 make sure the right n^th root of unity is used. Line 11 does the first half, 0 to n/2 - 1, line 12 does the second half, n/2 to n-1. Note the w used in this loop is w_n^k  but  w_n^k+n/2 = w_n^k w_n^n/2  = - w_n^k .

The running time satisfies: T ( n ) = 2 T ( n/2 ) + Q (n) so T ( n ) = Q (n lg n)  where the 2 T is the 2 FFT's and the Q (n) is loops 10 - 13.

Interpolation

The DFT can be written as:

 y = V_n ( w_n⁰, w_n¹, w_n², ..., w_nⁿ ) a

the ( k, j ) entry of V_n is V_n|_{( k, j )} = w_n^kj we can interpolate by inverting:

a = V_n^-1 ( w_n⁰, w_n¹, w_n², ..., w_nⁿ ) y

   = DFT_n^-1 ( y )

But it is easy to compute V_n^-1.

Theorem:

For j, k = 0, 1, ..., n - 1  V_n^-1|_{( k, j )} = (w_n-^kj ) / n

Proof:

We show that with this definition V_n^-1V_n = I , the identity, or  V_n^-1V_n|_{( k, j )} = d ( j, j' ) = { 1 if j = j' or 0 otherwise.

=	n - 1 å j = 0   (wn-kj ) / n  wnkj-1

 

=  1/n

n - 1 å j = 0  wnk(j'-j)

if j j' then:

n - 1 å j = 0  wnk(j'-j)    =

n - 1 å j = 0  ( wnk(j'-j))k

= 0

by the summation lemma. If j' = j then w_n^k(j'-j) = w_n⁰ = 1 so:

1/n

n - 1 å j = 0  wnk(j'-j) =

n - 1 å j = 0  1

= n/n = 1

 

Thus aj = 1/n

n - 1 å j = 0   yk (wn-kj )

which is like a DFT except:

1. role of a and y are reversed
2. w_n is replaced by w_n^-1
3. the result is devided by n

thus we can perform this in  Q (n lg n) with  a suitably modified Recursive-FFT. Call this:

 a = DFT_n^-1 ( y )

Convolution Theorem:

a Ä b = DFT_2n^-1 ( DFT_2n^-1 ( a ) ^. DFT_2n^-1 ( b )) , Ä is polynomial multiplication