Selection in Worst-Case Linear Time

Here we change select to guarantee a good split.

The Select algorithm determines the i^th smallest of an input array of n elements by executing the following steps:

1. Divide the n elements of the input array into ë n/5 û groups of 5 elements each and at most one group made up of the remaining n mod 5 elements.

2. Find the median of each of the é n/5 ù groups by insertion sorting the elements of each group (of which there are 5 at most) and taking its middle element. (If the group has an even number of elements, take the larger of the two medians.)

3. Use Select recursively to find the median x of the é n/5 ù medians found in step 2.

4. Partition the input array around the median-of-medians x using a modified version of Partition. Let k be the number of elements on the low side of the partition, so that n - k is the  number of elements on the high side.

5. Use Select recursively to find the i^th smallest element on the low side if i £ k, or the ( i - k)^th smallest element on the high side if i > k.

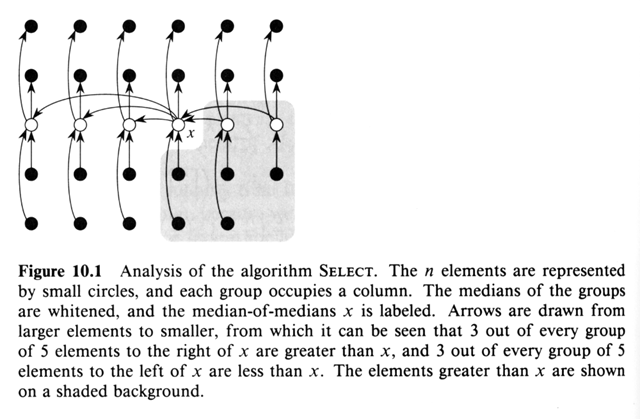
How many elements are greater than x?

1. Half the medians, or half of the  é n/5 ù  groups contribute 3 elements greater than x
2. Except the "mod" group and the group with x itself.

3 (  é1/2 é n/5 ù ù - 2 ) £ 3 n / 10 - 6

Where the 1/2 is half the medians,  é n/5 ù is the number of elements less than x, and the 2 is the "other" groups.

Must perform recursion  on Select   (7n / 10 + 6)

Step 1, 2, 4 ® O ( n )

Step 3         ® T ( é n/5 ù )

Step 5         ® T ( 7 n / 10 + 6 )

T ( n ) = T ( é n/5 ù ) + T ( 7 n / 10 + 6 ) + O ( n )

We show the run time is linear by substitution.

T ( n ) £ n c , substitute

T ( n ) £ c +  é n/5 ù + ( 7 c n / 10 + c 6 ) + O ( n )

£  n c / 5 + c + 7 c n / 10 + 6 c + O ( n )

£ 9/10 c n + 7 c + O ( n )

£  c n , when c ( n/10 - 7 ) > O ( n )

T ( n ) = O ( n )